Projet Deep Learning: Domineering
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
import keras
import random
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D
from sklearn.utils import shuffle
import time
import seaborn as sns
import dill
Using TensorFlow backend.
filename = 'globalsave2.pkl'
filename = 'globalsave20191808.pkl'
dill.dump_session(filename)
dill.load_session(filename)
https://machinelearningmastery.com/grid-search-hyperparameters-deep-learning-models-python-keras/
Réseau initial
Les données sont transformées pour être ensuite présentées au réseau.
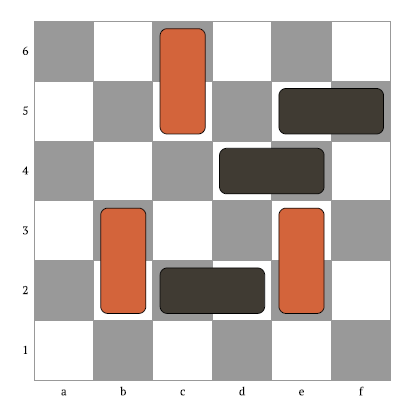
Une ligne du dataset est transformée en matrice à 3 dimensions (8,8,3)
- La première matrice représente le board en deux dimensions (8,8) vu du joueur vertical. Les cases que le joueur peut -jouer sont 0 et les cases déjà jouées sont 1.
- La seconde matrice représente le board vu du joueur horizontal. Les cases que le joueur peut jouer sont marquées 1 et les cases déjà jouées sont marquées 0.
- La troisième matrice est une matrice de 0 si le tour est pour le joueur vertical et 1 si le tour est pour le joueur horizontal.
L’output est une matrice nulle (8,8) sauf pour la position à jouer (la première des deux cases)
Nous entrainons un réseau de neurones convolutif 3D
- 1 couche d’entrée Conv2D-Relu avec un filtre (3,3) et 64 plans
- 5 couches de convolution Conv2D-Relu cachées
- 1 dernière couche entièrement connectée (Fully Connected) à la sortie avec activation softmax car nous entrainons le réseau pour une classification multiclasses à un seul label(chacune des classes est une case à jouer sur le board)
callbacks_list = [ keras.callbacks.EarlyStopping( monitor='val_acc', patience=3, )]
def get_model(board_size):
model = Sequential()
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu', input_shape=(board_size, board_size, 3), padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
def prepare_data(row, board_size):
board = row[:board_size**2]
flipped_board = row[board_size**2:2*board_size**2]
turn = row[2*board_size**2:3*board_size**2]
output = row[3*board_size**2:]
board = np.array(board).reshape((board_size, board_size))
flipped_board = np.array(flipped_board).reshape((board_size, board_size))
turn = np.array(turn).reshape((board_size, board_size))
output = np.array(output)
state = np.zeros((board_size, board_size, 3))
state[:,:,0] = board
state[:,:,1] = flipped_board
state[:,:,2] = turn
return state, output
Les données sont lues du fichier csv et séparées en un ensemble d’entrainement (70%) et un ensemble de test (30%).
Nous prenons les dernières lignes pour le test.
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
df=shuffle(df)
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
model = get_model(board_size)
Nous entrainons le réseau sur 20 époques avec un ensemble de valiation de 10% du Train
history=model.fit(X_train, Y_train, validation_split=0.1, epochs=20,#callbacks=callbacks_list
)
Train on 17737 samples, validate on 1971 samples
Epoch 1/20
17737/17737 [==============================] - 13s 751us/step - loss: 3.2563 - acc: 0.1806 - val_loss: 2.1669 - val_acc: 0.4485
Epoch 2/20
17737/17737 [==============================] - 5s 274us/step - loss: 1.8984 - acc: 0.4774 - val_loss: 1.8267 - val_acc: 0.4810
Epoch 3/20
17737/17737 [==============================] - 5s 275us/step - loss: 1.6791 - acc: 0.5162 - val_loss: 1.8228 - val_acc: 0.4957
Epoch 4/20
17737/17737 [==============================] - 5s 273us/step - loss: 1.5625 - acc: 0.5459 - val_loss: 1.7327 - val_acc: 0.4992
Epoch 5/20
17737/17737 [==============================] - 5s 272us/step - loss: 1.4640 - acc: 0.5685 - val_loss: 1.7564 - val_acc: 0.4911
Epoch 6/20
17737/17737 [==============================] - 5s 277us/step - loss: 1.3698 - acc: 0.5902 - val_loss: 1.8182 - val_acc: 0.4901
Epoch 7/20
17737/17737 [==============================] - 5s 272us/step - loss: 1.2638 - acc: 0.6237 - val_loss: 1.9405 - val_acc: 0.4835
Epoch 8/20
17737/17737 [==============================] - 5s 277us/step - loss: 1.1473 - acc: 0.6598 - val_loss: 2.0468 - val_acc: 0.4784
Epoch 9/20
17737/17737 [==============================] - 5s 271us/step - loss: 1.0394 - acc: 0.6894 - val_loss: 2.0847 - val_acc: 0.4718
Epoch 10/20
17737/17737 [==============================] - 5s 256us/step - loss: 0.9143 - acc: 0.7284 - val_loss: 2.5447 - val_acc: 0.4739
Epoch 11/20
17737/17737 [==============================] - 5s 259us/step - loss: 0.8015 - acc: 0.7665 - val_loss: 2.5733 - val_acc: 0.4612
Epoch 12/20
17737/17737 [==============================] - 5s 256us/step - loss: 0.7034 - acc: 0.7940 - val_loss: 2.7371 - val_acc: 0.4581
Epoch 13/20
17737/17737 [==============================] - 5s 259us/step - loss: 0.6151 - acc: 0.8241 - val_loss: 3.2355 - val_acc: 0.4658
Epoch 14/20
17737/17737 [==============================] - 5s 258us/step - loss: 0.5473 - acc: 0.8442 - val_loss: 3.5402 - val_acc: 0.4708
Epoch 15/20
17737/17737 [==============================] - 5s 256us/step - loss: 0.4978 - acc: 0.8589 - val_loss: 3.7355 - val_acc: 0.4592
Epoch 16/20
17737/17737 [==============================] - 5s 261us/step - loss: 0.4572 - acc: 0.8687 - val_loss: 4.0398 - val_acc: 0.4597
Epoch 17/20
17737/17737 [==============================] - 5s 258us/step - loss: 0.4292 - acc: 0.8767 - val_loss: 4.3756 - val_acc: 0.4455
Epoch 18/20
17737/17737 [==============================] - 5s 258us/step - loss: 0.4062 - acc: 0.8831 - val_loss: 4.5261 - val_acc: 0.4531
Epoch 19/20
17737/17737 [==============================] - 5s 257us/step - loss: 0.3880 - acc: 0.8912 - val_loss: 4.5565 - val_acc: 0.4521
Epoch 20/20
17737/17737 [==============================] - 5s 261us/step - loss: 0.3707 - acc: 0.8955 - val_loss: 4.6302 - val_acc: 0.4592
def plot_history(history):
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
plt.clf() #Clears the figure
acc = history_dict['acc']
val_acc = history_dict['val_acc']
plt.plot(epochs, acc, 'bo', label='Training acc')
plt.plot(epochs, val_acc, 'b', label='Validation acc')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
plot_history(history)


Réentrainons le modèle avec le nombre d’époques qui minimise l’erreur sur l’ensemble de validation
model = get_model(board_size)
history=model.fit(X_train, Y_train, validation_split=0.1, epochs=5)
NN_initial_no_augmentation_17k = model
Train on 17737 samples, validate on 1971 samples
Epoch 1/5
17737/17737 [==============================] - 6s 336us/step - loss: 3.5094 - acc: 0.1202 - val_loss: 2.3372 - val_acc: 0.3983
Epoch 2/5
17737/17737 [==============================] - 5s 256us/step - loss: 1.9539 - acc: 0.4623 - val_loss: 1.8288 - val_acc: 0.4860
Epoch 3/5
17737/17737 [==============================] - 5s 260us/step - loss: 1.6987 - acc: 0.5128 - val_loss: 1.7652 - val_acc: 0.5063
Epoch 4/5
17737/17737 [==============================] - 5s 255us/step - loss: 1.5786 - acc: 0.5368 - val_loss: 1.8154 - val_acc: 0.4886
Epoch 5/5
17737/17737 [==============================] - 5s 256us/step - loss: 1.4839 - acc: 0.5622 - val_loss: 1.7867 - val_acc: 0.4911
plot_history(history)


Nous pouvons alors faire les prédictions sur l’ensemble de test
pred_test = model.predict(X_test)
acc = accuracy_score(np.argmax(Y_test, axis=1), np.argmax(pred_test, axis=1))
print("Accuracy : %s " %acc)
Accuracy : 0.4802888599502782
Nous obtenons une accuracy sur le test à 0.493
Data augmentation
Nous allons essayer d’améliorer ce score par une Data augmentation.
Nous utiliserons trois symétries:
- le board vu en miroir. Nous utilsons la fonction prepare_data_lr qui retourne le board dans le sens gauche-droite
- le board vu de bas en haut. Nous utilisons la fonction prepare_data_ud qui retourne le board de bas en haut.
- le board tourné à 90. Nous utilisons la fonction prepare_data_90 qui fait une rotation à 90 du board. Le joueur vertical devient horizontal et inversement
import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
import keras
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D
def prepare_data_lr(row, board_size):
data = prepare_data(row, board_size)
state = data[0]
state = np.fliplr(state)
output = data[1]
output = np.array(output).reshape((board_size, board_size)) #on retourne l'output
output = np.fliplr(output)
player = int(state[:, :, 2][0][0])
if player == 0: # joueur vertical rien ne change pour l'output
output = output.ravel()
return state, output
if player == 1: # joueur horizental
permutation = [7, 0, 1, 2, 3, 4, 5, 6] # le 1 se retrouve sur la dernière case à jouer on permute pour avoir la première case
i = np.argsort(permutation)
output_moved = output[:, i]
output_moved = output_moved.ravel()
return state, output_moved
def prepare_data_ud(row, board_size):
data = prepare_data(row, board_size)
state = data[0]
state = np.flipud(state)
output = data[1]
output = np.array(output).reshape((board_size, board_size)) #on retourne l'output
output = np.flipud(output)
player = int(state[:, :, 2][0][0])
if player == 1: # horizental
output = output
output = output.ravel()
return state, output
if player == 0: # vertical
output_moved = np.roll(output, 7, axis=0) # on décale pour avoir l'output sur la première case à jouer
output_moved = output_moved.ravel()
return state, output_moved
def prepare_data_90(row, board_size):
data = prepare_data(row, board_size)
state = data[0]
state = np.rot90(state,-1)
output = data[1]
output = np.array(output).reshape((board_size, board_size))
output = np.rot90(output,-1)
player = int(state[:, :, 2][0][0])
if player == 1: # horizontal devient vertical
var=state[:,:,1]
state[:,:,1]=state[:,:,0]
state[:,:,0]=var
state[:,:,2]=0
output = output
output = output.ravel()
return state, output
if player == 0: # vertical devient horizontal
var=state[:,:,0]
state[:,:,0]=state[:,:,1]
state[:,:,1]=var
state[:,:,2]=1
permutation = [7, 0, 1, 2, 3, 4, 5, 6] # le 1 se retrouve sur la dernière case à jouer on permute pour avoir la première case
i = np.argsort(permutation)
output_moved = output[:, i]
output_moved = output_moved.ravel()
return state, output_moved
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
df=shuffle(df)
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_lr = prepare_data_lr(t, board_size)
X.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
X.append(row_ud)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
row_lr = prepare_data_lr(t, board_size)
XT.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
XT.append(row_ud)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
XT=[]
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
X_test_na = np.array([k[0] for k in XT])
Y_test_na = np.array([k[1] for k in XT])
model = get_model(board_size)
callbacks_list = [ keras.callbacks.EarlyStopping( monitor='val_acc', patience=3, )]
history=model.fit(X_train, Y_train, validation_split=0.1, epochs=20,batch_size=64,callbacks=callbacks_list)
NN_initial_with_augmentation_70k = history
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 11s 159us/step - loss: 2.7303 - acc: 0.2675 - val_loss: 2.0390 - val_acc: 0.4053
Epoch 2/20
70948/70948 [==============================] - 10s 135us/step - loss: 1.8260 - acc: 0.4532 - val_loss: 1.8772 - val_acc: 0.4277
Epoch 3/20
70948/70948 [==============================] - 10s 135us/step - loss: 1.7206 - acc: 0.4806 - val_loss: 1.8080 - val_acc: 0.4532
Epoch 4/20
70948/70948 [==============================] - 10s 134us/step - loss: 1.6543 - acc: 0.4995 - val_loss: 1.7900 - val_acc: 0.4592
Epoch 5/20
70948/70948 [==============================] - 10s 135us/step - loss: 1.5961 - acc: 0.5169 - val_loss: 1.8013 - val_acc: 0.4546
Epoch 6/20
70948/70948 [==============================] - 10s 136us/step - loss: 1.5425 - acc: 0.5330 - val_loss: 1.8489 - val_acc: 0.4551
Epoch 7/20
70948/70948 [==============================] - 10s 137us/step - loss: 1.4869 - acc: 0.5478 - val_loss: 1.8489 - val_acc: 0.4573
plot_history(history)


def accuracy_test(model,X_test,Y_test,X_test_na,Y_test_na):
#Accuracy test augmenté
pred_test = model.predict(X_test)
acc = accuracy_score(np.argmax(Y_test, axis=1), np.argmax(pred_test, axis=1))
print("Accuracy Test augmenté: %s " %acc)
#Accuracy test non augmenté
pred_test = model.predict(X_test_na)
acc = accuracy_score(np.argmax(Y_test_na, axis=1), np.argmax(pred_test, axis=1))
print("Accuracy Test non augmenté: %s " %acc)
accuracy_test(model,X_test,Y_test,X_test_na,Y_test_na)
Accuracy Test augmenté: 0.4555167515094116
Accuracy Test non augmenté: 0.4412217355274062
On va tenter un meilleur score avec une seule symétrie
Data augmentation à 90
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
df=shuffle(df)
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
model = get_model(board_size)
callbacks_list = [ keras.callbacks.EarlyStopping( monitor='val_acc', patience=3, )]
history=model.fit(X_train, Y_train, validation_split=0.1, epochs=20,batch_size=64,callbacks=callbacks_list)
Train on 35474 samples, validate on 3942 samples
Epoch 1/20
35474/35474 [==============================] - 6s 180us/step - loss: 3.5004 - acc: 0.1178 - val_loss: 2.5808 - val_acc: 0.3057
Epoch 2/20
35474/35474 [==============================] - 5s 135us/step - loss: 1.9509 - acc: 0.4527 - val_loss: 1.8729 - val_acc: 0.4734
Epoch 3/20
35474/35474 [==============================] - 5s 136us/step - loss: 1.7155 - acc: 0.5025 - val_loss: 1.7527 - val_acc: 0.5038
Epoch 4/20
35474/35474 [==============================] - 5s 134us/step - loss: 1.6171 - acc: 0.5229 - val_loss: 1.7273 - val_acc: 0.5109
Epoch 5/20
35474/35474 [==============================] - 5s 137us/step - loss: 1.5413 - acc: 0.5449 - val_loss: 1.7581 - val_acc: 0.5101
Epoch 6/20
35474/35474 [==============================] - 5s 136us/step - loss: 1.4718 - acc: 0.5641 - val_loss: 1.7710 - val_acc: 0.5068
Epoch 7/20
35474/35474 [==============================] - 5s 135us/step - loss: 1.3996 - acc: 0.5821 - val_loss: 1.7795 - val_acc: 0.4977
plot_history(history)


accuracy_test(model,X_test,Y_test,X_test_na,Y_test_na)
Accuracy Test augmenté: 0.4813543269799929
Accuracy Test non augmenté: 0.5774831301053629
MaxPooling Dropout
Essayons d’introduire un subsampling par MaxPooling et une régularisation par Dropout
from keras.layers import MaxPooling2D,Dropout
from keras import backend as K
def get_model2(board_size):
model = Sequential()
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu',input_shape=(board_size, board_size,3), padding="same",data_format='channels_last'))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
model2 = get_model2(board_size)
history=model2.fit(X_train, Y_train, validation_split=0.1, epochs=20,batch_size=64,callbacks=callbacks_list)
Train on 35474 samples, validate on 3942 samples
Epoch 1/20
35474/35474 [==============================] - 8s 214us/step - loss: 3.9131 - acc: 0.0345 - val_loss: 3.8002 - val_acc: 0.0444
Epoch 2/20
35474/35474 [==============================] - 5s 149us/step - loss: 3.7429 - acc: 0.0527 - val_loss: 3.7040 - val_acc: 0.0568
Epoch 3/20
35474/35474 [==============================] - 5s 153us/step - loss: 3.6775 - acc: 0.0656 - val_loss: 3.5972 - val_acc: 0.0771
Epoch 4/20
35474/35474 [==============================] - 5s 150us/step - loss: 3.5372 - acc: 0.0989 - val_loss: 3.3407 - val_acc: 0.1613
Epoch 5/20
35474/35474 [==============================] - 5s 150us/step - loss: 3.2371 - acc: 0.1750 - val_loss: 2.9149 - val_acc: 0.2620
Epoch 6/20
35474/35474 [==============================] - 5s 152us/step - loss: 2.9394 - acc: 0.2603 - val_loss: 2.6447 - val_acc: 0.3529
Epoch 7/20
35474/35474 [==============================] - 5s 150us/step - loss: 2.7612 - acc: 0.3149 - val_loss: 2.4925 - val_acc: 0.3902
Epoch 8/20
35474/35474 [==============================] - 5s 150us/step - loss: 2.6408 - acc: 0.3484 - val_loss: 2.4229 - val_acc: 0.4127
Epoch 9/20
35474/35474 [==============================] - 5s 152us/step - loss: 2.5686 - acc: 0.3685 - val_loss: 2.3737 - val_acc: 0.4353
Epoch 10/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.4999 - acc: 0.3897 - val_loss: 2.3420 - val_acc: 0.4424
Epoch 11/20
35474/35474 [==============================] - 5s 150us/step - loss: 2.4591 - acc: 0.3974 - val_loss: 2.2998 - val_acc: 0.4462
Epoch 12/20
35474/35474 [==============================] - 5s 153us/step - loss: 2.4150 - acc: 0.4109 - val_loss: 2.2775 - val_acc: 0.4556
Epoch 13/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.3871 - acc: 0.4155 - val_loss: 2.2501 - val_acc: 0.4587
Epoch 14/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.3588 - acc: 0.4250 - val_loss: 2.2550 - val_acc: 0.4622
Epoch 15/20
35474/35474 [==============================] - 5s 153us/step - loss: 2.3305 - acc: 0.4300 - val_loss: 2.2388 - val_acc: 0.4630
Epoch 16/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.3084 - acc: 0.4349 - val_loss: 2.2163 - val_acc: 0.4642
Epoch 17/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.3013 - acc: 0.4379 - val_loss: 2.2186 - val_acc: 0.4673
Epoch 18/20
35474/35474 [==============================] - 5s 153us/step - loss: 2.2864 - acc: 0.4418 - val_loss: 2.2137 - val_acc: 0.4675
Epoch 19/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.2714 - acc: 0.4461 - val_loss: 2.2067 - val_acc: 0.4739
Epoch 20/20
35474/35474 [==============================] - 5s 151us/step - loss: 2.2553 - acc: 0.4495 - val_loss: 2.2154 - val_acc: 0.4729
plot_history(history)


accuracy_test(model2,X_test,Y_test,X_test_na,Y_test_na)
Accuracy Test augmenté: 0.4768556884100864
Accuracy Test non augmenté: 0.5085829288504795
Supprimons le Max Pooling car on perd peut être l’information de la structure du jeu
from keras.layers import MaxPooling2D,Dropout
from keras import backend as K
def get_model3(board_size):
model = Sequential()
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu',input_shape=(board_size, board_size,3), padding="same",data_format='channels_last'))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(0.3))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
df=shuffle(df)
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
model3 = get_model3(board_size)
history=model3.fit(X_train, Y_train, validation_split=0.1, epochs=20,batch_size=64,callbacks=callbacks_list)
Train on 35474 samples, validate on 3942 samples
Epoch 1/20
35474/35474 [==============================] - 7s 210us/step - loss: 3.8382 - acc: 0.0467 - val_loss: 3.6905 - val_acc: 0.0583
Epoch 2/20
35474/35474 [==============================] - 6s 155us/step - loss: 2.6674 - acc: 0.2911 - val_loss: 2.1071 - val_acc: 0.4239
Epoch 3/20
35474/35474 [==============================] - 5s 154us/step - loss: 2.0039 - acc: 0.4378 - val_loss: 1.8324 - val_acc: 0.4845
Epoch 4/20
35474/35474 [==============================] - 5s 153us/step - loss: 1.8658 - acc: 0.4709 - val_loss: 1.7907 - val_acc: 0.4866
Epoch 5/20
35474/35474 [==============================] - 6s 156us/step - loss: 1.7927 - acc: 0.4839 - val_loss: 1.7753 - val_acc: 0.4906
Epoch 6/20
35474/35474 [==============================] - 5s 153us/step - loss: 1.7384 - acc: 0.4967 - val_loss: 1.7576 - val_acc: 0.4911
Epoch 7/20
35474/35474 [==============================] - 5s 153us/step - loss: 1.6970 - acc: 0.5051 - val_loss: 1.7511 - val_acc: 0.4909
Epoch 8/20
35474/35474 [==============================] - 6s 155us/step - loss: 1.6683 - acc: 0.5136 - val_loss: 1.7251 - val_acc: 0.4949
Epoch 9/20
35474/35474 [==============================] - 5s 153us/step - loss: 1.6390 - acc: 0.5192 - val_loss: 1.7298 - val_acc: 0.4891
Epoch 10/20
35474/35474 [==============================] - 5s 154us/step - loss: 1.6198 - acc: 0.5241 - val_loss: 1.7275 - val_acc: 0.4868
Epoch 11/20
35474/35474 [==============================] - 6s 156us/step - loss: 1.5972 - acc: 0.5286 - val_loss: 1.7146 - val_acc: 0.4952
Epoch 12/20
35474/35474 [==============================] - 5s 154us/step - loss: 1.5832 - acc: 0.5349 - val_loss: 1.7323 - val_acc: 0.4893
Epoch 13/20
35474/35474 [==============================] - 5s 155us/step - loss: 1.5628 - acc: 0.5396 - val_loss: 1.7277 - val_acc: 0.4911
Epoch 14/20
35474/35474 [==============================] - 6s 161us/step - loss: 1.5411 - acc: 0.5432 - val_loss: 1.7233 - val_acc: 0.4871
plot_history(history)


model3 = get_model3(board_size)
model3.fit(X_train, Y_train, validation_split=0.1, epochs=8,batch_size=64,callbacks=callbacks_list)
Train on 35474 samples, validate on 3942 samples
Epoch 1/8
35474/35474 [==============================] - 8s 216us/step - loss: 3.7811 - acc: 0.0548 - val_loss: 3.5778 - val_acc: 0.0921
Epoch 2/8
35474/35474 [==============================] - 5s 155us/step - loss: 2.4671 - acc: 0.3324 - val_loss: 1.9977 - val_acc: 0.4495
Epoch 3/8
35474/35474 [==============================] - 5s 154us/step - loss: 1.9823 - acc: 0.4436 - val_loss: 1.8503 - val_acc: 0.4739
Epoch 4/8
35474/35474 [==============================] - 5s 153us/step - loss: 1.8616 - acc: 0.4697 - val_loss: 1.7946 - val_acc: 0.4835
Epoch 5/8
35474/35474 [==============================] - 6s 156us/step - loss: 1.7947 - acc: 0.4819 - val_loss: 1.7774 - val_acc: 0.4779
Epoch 6/8
35474/35474 [==============================] - 5s 154us/step - loss: 1.7398 - acc: 0.4962 - val_loss: 1.8450 - val_acc: 0.4678
Epoch 7/8
35474/35474 [==============================] - 5s 155us/step - loss: 1.7006 - acc: 0.5047 - val_loss: 1.7431 - val_acc: 0.4929
Epoch 8/8
35474/35474 [==============================] - 6s 156us/step - loss: 1.6773 - acc: 0.5101 - val_loss: 1.7386 - val_acc: 0.4934
<keras.callbacks.History at 0x1c4abe83f60>
accuracy_test(model3,X_test,Y_test,X_test_na,Y_test_na)
Accuracy Test augmenté: 0.5061560317272404
Accuracy Test non augmenté: 0.5425594885758257
Essayons ce modèle sur le jeu augmenté des 3 symmétries
model3 = get_model3(board_size)
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_lr = prepare_data_lr(t, board_size)
X.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
X.append(row_ud)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train = np.array([k[0] for k in X])
Y_train = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
row_lr = prepare_data_lr(t, board_size)
XT.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
XT.append(row_ud)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test = np.array([k[0] for k in XT])
Y_test = np.array([k[1] for k in XT])
history=model3.fit(X_train, Y_train, validation_split=0.1, epochs=20,callbacks=callbacks_list)
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 24s 332us/step - loss: 3.1164 - acc: 0.1850 - val_loss: 2.1193 - val_acc: 0.3853
Epoch 2/20
70948/70948 [==============================] - 21s 299us/step - loss: 2.0518 - acc: 0.3962 - val_loss: 1.8910 - val_acc: 0.4335
Epoch 3/20
70948/70948 [==============================] - 21s 302us/step - loss: 1.9188 - acc: 0.4307 - val_loss: 1.8193 - val_acc: 0.4463
Epoch 4/20
70948/70948 [==============================] - 21s 300us/step - loss: 1.8725 - acc: 0.4422 - val_loss: 1.7830 - val_acc: 0.4618
Epoch 5/20
70948/70948 [==============================] - 21s 302us/step - loss: 1.8393 - acc: 0.4518 - val_loss: 1.7815 - val_acc: 0.4585
Epoch 6/20
70948/70948 [==============================] - 21s 303us/step - loss: 1.8206 - acc: 0.4592 - val_loss: 1.7772 - val_acc: 0.4630
Epoch 7/20
70948/70948 [==============================] - 21s 302us/step - loss: 1.8102 - acc: 0.4590 - val_loss: 1.7661 - val_acc: 0.4627
Epoch 8/20
70948/70948 [==============================] - 22s 303us/step - loss: 1.8019 - acc: 0.4642 - val_loss: 1.7802 - val_acc: 0.4594
Epoch 9/20
70948/70948 [==============================] - 22s 306us/step - loss: 1.7987 - acc: 0.4648 - val_loss: 1.7637 - val_acc: 0.4628
plot_history(history)


accuracy_test(model3,X_test,Y_test,X_test_na,Y_test_na)
Accuracy Test augmenté: 0.47297857227418016
Accuracy Test non augmenté: 0.4833668758138984
Conclusion
Nous retenons le modèle sans MaxPooling avec Dropout (modèle 3) entrainé sur le jeu de données augmenté avec la symmétrie à 90 degrés. C’est le réseau qui donne la meilleure accuracy à la fois sur le Test initial et le Test augmenté. Le premier réseau donne également des résultats similaires mais sans Data Augmentation.
PARTIE II - Jeux etc.
Code pour jouer la partie
Nous tentons maintenant de faire jouer nous différents réseaux afin : de les confronter aux règles de jeux, et voir si le réseau de prédit pas dénouer des coups qui ne serait pas possibles. De tester si et comment l’accuracy se traduit en capacité de gagner le jeu. … Pour cela on commencer par tester le NN contre un bot jouant de façon aléatoire.
player = 1 : Horizontal (H) player = 2 : Vertical (V)
Code pour jouer les parties standard :
- Évaluer les coups possibles
- Choisir un coup à jouer (random ou par Monte Carlo)
- Jouer le coup, ie: mettre à jours le damier
- jouer une partie complète et retourner le vainqueur Au global:
- Un bot random : qui joue aléatoirement
- un bot Monte Carlo (noté MC): qui va réaliser un nombre d’itération définit et tester des possibilités de jeux qui mennent à la victoire, le coup choisi pour etre joué est celui dont le nombres de victoire est le plus important dans les multiples chaines joués.
import random
from random import randint
def coup_H(A,i,j):
if A[i,j] == 0 and A[i+1,j] == 0:
A[i,j] = 1
A[i+1,j] = 1
def coup_V(A,i,j):
if A[i,j] == 0 and A[i,j+1] == 0:
A[i,j] = 2
A[i,j+1] = 2
def coups_possibles_H(A):
liste_possible = []
for i in range(0,len(A)-1):
for j in range(0,len(A)):
if A[i,j] ==0 and A[i+1,j] == 0:
liste_possible.append((i,j))
return liste_possible
def coups_possibles_V(A):
liste_possible = []
for i in range(0,len(A)):
for j in range(0,len(A)-1):
if A[i,j] ==0 and A[i,j+1] == 0:
liste_possible.append((i,j))
return liste_possible
def rand_domineering(A, player):
while 1:
if player == 1:
if coups_possibles_H(A) != []:
play = random.choice(coups_possibles_H(A))
coup_H(A, play[0], play[1])
player = 2
else:
return player
if player == 2:
if coups_possibles_V(A) != []:
play = random.choice(coups_possibles_V(A))
coup_V(A, play[0], play[1])
player = 1
else:
return player
def mc_domineering(A, player,niter):
while 1:
if player == 1:
if coups_possibles_H(A) != []:
play = montecarlo(A, player,niter)
coup_H(A, play[0], play[1])
player = 2
else:
return player
if player == 2:
if coups_possibles_V(A) != []:
play = montecarlo(A, player,niter)
coup_V(A, play[0], play[1])
player = 1
else:
return player
def montecarlo(A, player, niter) :
B = np.copy(A)
if player == 1:
moves = coups_possibles_H(B)
if moves != []:
for coup in moves:
victoire = np.zeros(len(moves))
for i in range(0,niter):
coup_H(B, coup[0], coup[1])
loser = rand_domineering(B, 2)
if loser == 2:
victoire[moves.index(coup)] = victoire[moves.index(coup)] + 1
if player == 2:
moves = coups_possibles_V(B)
if moves != []:
for coup in moves:
victoire = np.zeros(len(moves))
for i in range(0,niter):
coup_V(B, coup[0], coup[1])
loser = rand_domineering(B, 1)
if loser == 1:
victoire[moves.index(coup)] = victoire[moves.index(coup)] + 1
victoire = victoire / niter
max = 0
for i in range(0, len(victoire)):
if victoire[i] > max:
max = victoire[i]
coupchoisi = moves[i]
return coupchoisi
def rand_vs_mc_domineering(A, player,niter):
while 1:
if player == 1:
if coups_possibles_H(A) != []:
play = montecarlo(A, player,niter)
coup_H(A, play[0], play[1])
player = 2
else:
return player
if player == 2:
if coups_possibles_V(A) != []:
play = random.choice(coups_possibles_V(A))
coup_V(A, play[0], play[1])
player = 1
else:
return player
Faisont jouer ensemble les BOTs:
- Random VS Ramdom
- Random VS MC
- MC VS MC
niter = 100 #itération de MC
ngame = 10 #nombres de parties
losers_Ran_VS_Ran = []
losers_Ran_VS_MC = []
losers_MC_VS_MC = []
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_Ran_VS_Ran.append(rand_domineering(damier, player))
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_MC_VS_MC.append(mc_domineering(damier, player,niter))
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_Ran_VS_MC.append(rand_vs_mc_domineering(damier, player,niter))
print("Random VS Ramdom Joueur 1 perd (%): ",100*np.count_nonzero( np.array(losers_Ran_VS_Ran) == 1)/ngame)
print("Random VS MC Joueur 1 perd (%): ",100*np.count_nonzero( np.array(losers_Ran_VS_MC) == 1)/ngame)
print("MC VS MC Joueur 1 perd (%): ",100*np.count_nonzero( np.array(losers_MC_VS_MC) == 1)/ngame)
Random VS Ramdom Joueur 1 perd (%): 70.0
Random VS MC Joueur 1 perd (%): 80.0
MC VS MC Joueur 1 perd (%): 100.0
Commentaire …
Partie joués avec les réseaux de neurones (NN) VS Bots
Code spécifique pour jouer les parties
Afin de pouvoir utiliser les réseaux que l’on a entrainés nous avons :
- Remettre le damier dans un format de données compatible (comme pour le train/test)
- Adapter le code, notamment pour éviter que le NN joue à des positions qu’il n’a pas de droit. En effet en faisant des tests on a remarqué que les réseaux tentent des coups qui ne sont pas possibles, notamment lorsque le damier commence à être beaucoup rempli
Nous avons choisi de tester les bots contre le réseau modèle3 : sans MaxPooling avec Dropout et entrainé sur le jeu de données augmenté avec la symmétrie à 90 degrés
#remetre l'etat de jeu compréhensible par le NN
def f(a):
if a>0:
return 1
return 0
def to_bool(xx):
x = xx.ravel()
return np.fromiter((f(xi) for xi in x), x.dtype).reshape(8,8)
def swap_player(xx):
x = xx.ravel()
return np.fromiter((np.where(xi==0,1,0) for xi in x), x.dtype).reshape(8,8)
def coup_NN(A,player,NN_name):
state = np.zeros((1, 8, 8, 3))
state[0,:,:,0] = to_bool(A)
state[0,:,:,1] = swap_player(state[0,:,:,0])
if player == 2 :
state[0,:,:,2] = np.ones((8,8) ,dtype=np.int16)
pos = np.argmax(NN_name.predict(state))
return (pos // 8, pos % 8 )
Réseau de neurone (NN) VS random bot
ngame = 2000
#jouer contre un bot random
def rand_VS_NN(A, player, NN_name):
nb_bad = 0
while 1:
if player == 1:
if coups_possibles_H(A) != []:
# print(A)
play = coup_NN(A,player,NN_name)
# print(play)
if play[0] > 6:
play = random.choice(coups_possibles_H(A))
nb_bad = nb_bad + 1
coup_H(A, play[0], play[1])
player = 2
else:
return (player,nb_bad)
if player == 2:
if coups_possibles_V(A) != []:
play = random.choice(coups_possibles_V(A))
coup_V(A, play[0], play[1])
player = 1
else:
return (player,nb_bad)
losers_ranNN = []
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_ranNN.append(rand_VS_NN(damier, player,model3))
print("In Random Domineering, NN loses (%) : ",100*np.count_nonzero( np.array(losers_ranNN)[:,0] == 1)/ngame)
print(" En moyenne le NN tente de jouer XX coups impossibles par partie", sum (np.array(losers_ranNN)[:,1])/ngame)
In Random Domineering, NN loses (%) : 0.2
En moyenne le NN tente de jouer XX coups impossibles par partie 0.0
On constate que:
- Le NN perd quand même quelques rares fois contre un bot qui joue aléatoirement (environ 0,2%)
- le NN tente également de jouer dans des positions qui ne font pas partie des coups possibles (dernières ligne ou colonnes, ou carrément à des endroits où il n’y a pas de place) : Ce phénomène est relativement dérangeant, car on n’a jamais appris au réseau à jouer de cette manière. Même si l’acurracy est seulement de 0.5 on aura pu penser que le réseau avait « au moins » compris qu’il ne pouvait pas jouer dans les endroits déjà prie.
Afin de corriger ce, en cas de prédiction de coup impossible, on remplace encore une fois par un coup aléatoire.
On test maintenant contre un bot monte-carlo : ie un bot qui va tester plusieurs combinaison et ne retenir que les coup qui mènent à une victoire
NN VS MC
Le code est adapté pour faire jouer le NN ans les deux sens: vertival et horizontal. Cela permet de vérifier que le comportement est similaire dans ces deux cas.
def MC_VS_NN1(A, player, NN_name, niter):
nb_bad = 0
while 1:
if player == 1:
cpH = coups_possibles_H(A)
if cpH != []:
play = coup_NN(A,player,NN_name)
if (play not in cpH):
play = random.choice(cpH)
nb_bad = nb_bad + 1
coup_H(A, play[0], play[1])
player = 2
else:
return (player,nb_bad)
if player == 2:
if coups_possibles_V(A) != []:
play = montecarlo(A, player, niter)
coup_V(A, play[0], play[1])
player = 1
else:
return (player,nb_bad)
def MC_VS_NN2(A, player, NN_name, niter):
nb_bad = 0
while 1:
if player == 2:
cpV = coups_possibles_V(A)
if cpV != []:
play = coup_NN(A,player,NN_name)
if (play not in cpV):
play = random.choice(cpV)
nb_bad = nb_bad + 1
coup_V(A, play[0], play[1])
player = 1
else:
return (player,nb_bad)
if player == 1:
if coups_possibles_H(A) != []:
play = montecarlo(A, player, niter)
coup_H(A, play[0], play[1])
player = 2
else:
return (player,nb_bad)
ngame = 20
niter = 500 #pour MC
losers_MCNN1 = []
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_MCNN1.append(MC_VS_NN1(damier, player,model3, niter))
print("In MC Domineering, NN (vertical) loses (%) : ",100*np.count_nonzero( np.array(losers_MCNN1)[:,0] == 1)/ngame)
print(" En moyenne le NN tente de jouer ", sum (np.array(losers_MCNN1)[:,1])/ngame , " coups impossibles par partie")
losers_MCNN2 = []
for i in range(0,ngame):
player = randint(1,2)
damier = np.zeros((8, 8))
losers_MCNN2.append(MC_VS_NN2(damier, player,model3, niter))
print("In MC Domineering, NN (horizontal) loses (%) : ",100*np.count_nonzero( np.array(losers_MCNN2)[:,0] == 2)/ngame)
print(" En moyenne le NN tente de jouer ", sum (np.array(losers_MCNN2)[:,1])/ngame , " coups impossibles par partie")
In MC Domineering, NN (vertical) loses (%) : 50.0
En moyenne le NN tente de jouer 0.0 coups impossibles par partie
In MC Domineering, NN (horizontal) loses (%) : 0.0
En moyenne le NN tente de jouer 0.0 coups impossibles par partie
Constats de NN VS MC :
- le réseau bat systématiquement le bot MC, peu importe la position de jeux
- Même en augmentant le nombre d’itérations de MC, le NN gagne toujours.
Le réseau a été entrainé à l’aide d’un jeu de données issues de parties jouées avec du Monte-Carlo (pour trouver le meilleur coup à jouer). Mais nous n’avons pas exactement plus de détail sur le données. Le fait que le réseau soit toujours meilleur laisse penser que :
- les coups du jeu d’entrainement sont de « bonnes qualités » , c.-à-d. générées avec beaucoup d’itération de Monte-Carlo. Et donc peu être qu’en augmentant beaucoup niter on aurait un bot MC gagnant. Nous avons testé jusqu’ à 500 itérations, sans succès.
Remarque : NN VS Bots
- Le NN gagne toutes les parties lorsqu’il joue contre des bot MC
- le NN perds quelques parties lorsqu’il joue contre des bot aléatoire, il tente également des coups interdit
Cela illustre bien le défaut connu des NN à gérer des situations nouvelles pour lequel il n’a pas été entrainé (car le jeu d’entrainement est issu de simulation de Monte Carlo).
Affrontement entre les NN et réutilisation des coups gagnants
Dans cette partie on va faire jouer plusieurs NN les uns contre les autres afin de :
- Comprendre quelle structure de réseau est plus performante
- Voir comment l’accuracy et le fait de gagner les parties sont liés (ou pas)
- Réutiliser les historiques des parties pour augmenter le train
le code suivant sert à jouer des parties NN VS NN ou NN VS MC en conservant les coups joués par le vainqueur
#pour chaque coups retourne l'etat du board en format NN et la position choisi par le Réseau
def ReturnPlayForHist(A,player,NN_name, play):
state = np.zeros((1, 8, 8, 3))
state[0,:,:,0] = to_bool(A)
state[0,:,:,1] = swap_player(state[0,:,:,0])
if player == 2 :
state[0,:,:,2] = np.ones((8,8) ,dtype=np.int16)
pos = play[0] + 8*play[1]
pos_v = np.zeros(64)
pos_v[pos] = 1
return (state[0,:,:,0],state[0,:,:,1],state[0,:,:,2],pos_v)
#Meme fonction que précédement mais retroune égalemement l'historique (du vainqueur)
def MC_VS_NN1_histo(A, player, NN_name, niter,name):
nb_bad = 0
Historique1 = []
Historique2 = []
while 1:
if player == 1:
cpH = coups_possibles_H(A)
if cpH != []:
play = coup_NN(A,player,NN_name)
if (play not in cpH):
play = random.choice(cpH)
nb_bad = nb_bad + 1
Historique1.append(ReturnPlayForHist(A,player,NN_name,play))
coup_H(A, play[0], play[1])
player = 2
else:
# print(PassHisto)
return (name,nb_bad),Historique2
if player == 2:
if coups_possibles_V(A) != []:
play = montecarlo(A, player, niter)
Historique2.append(ReturnPlayForHist(A,player,"MC_Algo",play))
coup_V(A, play[0], play[1])
player = 1
else:
PassHisto = Historique1
#print(PassHisto)
return ("MC_Algo",nb_bad),Historique1
def MC_VS_NN2_histo(A, player, NN_name, niter,name):
nb_bad = 0
Historique1 = []
Historique2 = []
while 1:
if player == 2:
cpV = coups_possibles_V(A)
if cpV != []:
play = coup_NN(A,player,NN_name)
if (play not in cpV):
play = random.choice(cpV)
nb_bad = nb_bad + 1
Historique1.append(ReturnPlayForHist(A,player,NN_name,play))
coup_V(A, play[0], play[1])
player = 1
else:
return (name,nb_bad),Historique2
if player == 1:
if coups_possibles_H(A) != []:
play = montecarlo(A, player, niter)
Historique2.append(ReturnPlayForHist(A,player,"MC_Algo",play))
coup_H(A, play[0], play[1])
player = 2
else:
return ("MC_Algo",nb_bad),Historique1
def NN_VS_NN(A, player, NN_name1, NN_name2, NN_name1STR, NN_name2STR):
nb_bad = 0
Historique1 = []
Historique2 = []
while 1:
if player == 1:
cpH = coups_possibles_H(A)
if cpH != []:
play = coup_NN(A,player,NN_name1)
if (play not in cpH):
play = random.choice(cpH)
nb_bad = nb_bad + 1
Historique1.append(ReturnPlayForHist(A,player,NN_name1,play))
coup_H(A, play[0], play[1])
player = 2
else:
return (NN_name1STR,nb_bad),Historique2
if player == 2:
cpV = coups_possibles_V(A)
if cpV != []:
play = coup_NN(A,player,NN_name2)
if (play not in cpV):
play = random.choice(cpV)
nb_bad = nb_bad + 1
Historique2.append(ReturnPlayForHist(A,player,NN_name2,play))
coup_V(A, play[0], play[1])
player = 1
else:
return (NN_name2STR,nb_bad),Historique1
Choix de l’architecture des réseaux
le code suivant sert à jouer des parties NN VS NN ou NN VS MC en conservant les coups joués par le vainqueur
nous avons remis le code des modèles déjà détaillés en partie I (pour plus de lisibilité)
Les modèles utilisés pour la suite seront :
- le modèle de base : 6 couches denses Conv2D
- le modèle dropout_01: idem avec un dropout sur chaque couche de 0.1
- le modèle dropout_03: idem avec un dropout sur chaque couche de 0.3
- le modèle dropout_L: idem avec un dropout variable de 0.1 en entrée et 0.3 en sortie par pas de 0.05
Ces 4 modèles sont entrainés :
- une fois sans Data Augmentation (DA)
- une fois avec DA
Soit 8 réseaux au total
# liste des modèles:
cstboard_size = 8
def get_model_base(board_size = cstboard_size):
model = Sequential()
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu', input_shape=(board_size, board_size, 3), padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
def get_model_dropout_01(board_size = cstboard_size):
model = Sequential()
droprate = .1
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu',input_shape=(board_size, board_size,3), padding="same",data_format='channels_last'))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
def get_model_dropout_03(board_size = cstboard_size):
model = Sequential()
droprate = .3
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu',input_shape=(board_size, board_size,3), padding="same",data_format='channels_last'))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(droprate))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
def get_model_dropout_L(board_size = cstboard_size):
model = Sequential()
model.add(Conv2D(64, kernel_size=(3, 3), activation='relu',input_shape=(board_size, board_size,3), padding="same",data_format='channels_last'))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(.1))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(.15))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(.2))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(.25))
model.add(Conv2D(64, (3, 3), activation='relu', padding="same"))
model.add(Dropout(.3))
model.add(Flatten())
model.add(Dense(board_size**2, activation='softmax'))
model.compile(loss=keras.losses.categorical_crossentropy, optimizer=keras.optimizers.Adadelta(), metrics=['accuracy'])
return model
Pour plus de lisibilité le code pour la préparation des données et la data Augmentation est remis ici. Il servira également à traiter les données issues des historiques.
Nous avons choisi ici de ne pas augmenter les données pour le test, notamment car nous voulons tester les réseaux sur une base commune et donc avec un train sans DA pour tous
#augmenter le train
train_aug = False
#fichier original
filename = 'domineering.csv'
df = pd.read_csv(filename, sep=',', na_values=[""], header=None)
board_size = 8
df=shuffle(df)
data = df.values.tolist()
train = data[:int(0.7*len(data))]
test = data[int(0.7*len(data)):]
#train / test standard (no data augment)
def prepare_train_DA_NO(train,test):
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
X_train_DA_NO = np.array([k[0] for k in X])
Y_train_DA_NO = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
X_test_DA_NO = np.array([k[0] for k in XT])
Y_test_DA_NO = np.array([k[1] for k in XT])
return X_train_DA_NO,Y_train_DA_NO,X_test_DA_NO,Y_test_DA_NO
#train / test augmented (yes data augment)
def prepare_train_DA_YES(train,test):
X = []
for t in train:
row = prepare_data(t, board_size)
X.append(row)
row_lr = prepare_data_lr(t, board_size)
X.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
X.append(row_ud)
row_90=prepare_data_90(t,board_size)
X.append(row_90)
X_train_DA_YES = np.array([k[0] for k in X])
Y_train_DA_YES = np.array([k[1] for k in X])
XT = []
for t in test:
row = prepare_data(t, board_size)
XT.append(row)
if train_aug:
row_lr = prepare_data_lr(t, board_size)
XT.append(row_lr)
row_ud = prepare_data_ud(t, board_size)
XT.append(row_ud)
row_90=prepare_data_90(t,board_size)
XT.append(row_90)
X_test_DA_YES = np.array([k[0] for k in XT])
Y_test_DA_YES = np.array([k[1] for k in XT])
return X_train_DA_YES,Y_train_DA_YES,X_test_DA_YES,Y_test_DA_YES
def formathisto(HistoBrut):
return np.concatenate((HistoBrut[1][1][0].ravel(),HistoBrut[1][1][1].ravel(),HistoBrut[1][1][2].ravel(),HistoBrut[1][1][3].ravel()),axis=0)
X_train_DA_NO,Y_train_DA_NO,X_test_DA_NO,Y_test_DA_NO = prepare_train_DA_NO(train,test)
X_train_DA_YES,Y_train_DA_YES,X_test_DA_YES,Y_test_DA_YES = prepare_train_DA_YES(train,test)
- Génération des données de train et test
- Chargement des modèles définis précédemment dans une liste dans une liste
Model_list = []
Name_list = ["base","base_drop_01","base_drop_03","base_drop_L","baseDA","base_drop_01DA","base_drop_03DA","base_drop_LDA" ]
Model_list.append(get_model_base())
Model_list.append(get_model_dropout_01())
Model_list.append(get_model_dropout_03())
Model_list.append(get_model_dropout_L())
Model_list.append(get_model_base())
Model_list.append(get_model_dropout_01())
Model_list.append(get_model_dropout_03())
Model_list.append(get_model_dropout_L())
def Keras_training(Model,X_train,Y_train):
callbacks_list = [ keras.callbacks.EarlyStopping( monitor='val_acc', patience=3 )]
history=Model.fit(X_train, Y_train, validation_split=0.1, epochs=20,batch_size=128,callbacks=callbacks_list)
return history
Keras_training :
- Pour arrêter automatiquement l’entrainement, ici on choit 3 epoch
- Le nombre d’unités de calcul disponible sur la carte graphique permet de réduire le temps de calcul en augmentant le batch size. On ne préfère cependant pas trop l’augmenter pour garder une certaine cohérence dans l’apprentissage (de position précise…)
Historique_all = []
t = time.process_time()
Historique_all.append(Keras_training(Model_list[0],X_train_DA_NO,Y_train_DA_NO))
Historique_all.append(Keras_training(Model_list[1],X_train_DA_NO,Y_train_DA_NO))
Historique_all.append(Keras_training(Model_list[2],X_train_DA_NO,Y_train_DA_NO))
Historique_all.append(Keras_training(Model_list[3],X_train_DA_NO,Y_train_DA_NO))
Historique_all.append(Keras_training(Model_list[4],X_train_DA_YES,Y_train_DA_YES))
Historique_all.append(Keras_training(Model_list[5],X_train_DA_YES,Y_train_DA_YES))
Historique_all.append(Keras_training(Model_list[6],X_train_DA_YES,Y_train_DA_YES))
Historique_all.append(Keras_training(Model_list[7],X_train_DA_YES,Y_train_DA_YES))
end = time.time()
elapsed_time = time.process_time() - t
print(elapsed_time) #660sec with batch = 64 ; 430sec with batch = 128
Train on 17737 samples, validate on 1971 samples
Epoch 1/20
17737/17737 [==============================] - 4s 243us/step - loss: 3.8532 - acc: 0.0514 - val_loss: 3.6898 - val_acc: 0.0604
Epoch 2/20
17737/17737 [==============================] - 1s 78us/step - loss: 3.1957 - acc: 0.1747 - val_loss: 2.4978 - val_acc: 0.3420
Epoch 3/20
17737/17737 [==============================] - 1s 78us/step - loss: 2.0370 - acc: 0.4469 - val_loss: 1.9467 - val_acc: 0.4698
Epoch 4/20
17737/17737 [==============================] - 1s 76us/step - loss: 1.7694 - acc: 0.5024 - val_loss: 1.8729 - val_acc: 0.4718
Epoch 5/20
17737/17737 [==============================] - 1s 76us/step - loss: 1.6412 - acc: 0.5243 - val_loss: 1.8295 - val_acc: 0.4749
Epoch 6/20
17737/17737 [==============================] - 1s 76us/step - loss: 1.5500 - acc: 0.5483 - val_loss: 1.8252 - val_acc: 0.4805
Epoch 7/20
17737/17737 [==============================] - 1s 76us/step - loss: 1.4668 - acc: 0.5675 - val_loss: 1.8421 - val_acc: 0.4805
Epoch 8/20
17737/17737 [==============================] - 1s 76us/step - loss: 1.3793 - acc: 0.5944 - val_loss: 1.8973 - val_acc: 0.4698
Epoch 9/20
17737/17737 [==============================] - 1s 75us/step - loss: 1.2955 - acc: 0.6206 - val_loss: 1.9429 - val_acc: 0.4774
Epoch 10/20
17737/17737 [==============================] - 1s 75us/step - loss: 1.2021 - acc: 0.6420 - val_loss: 2.0866 - val_acc: 0.4642
Train on 17737 samples, validate on 1971 samples
Epoch 1/20
17737/17737 [==============================] - 4s 241us/step - loss: 3.8533 - acc: 0.0470 - val_loss: 3.7121 - val_acc: 0.0741
Epoch 2/20
17737/17737 [==============================] - 2s 90us/step - loss: 3.0977 - acc: 0.2023 - val_loss: 2.2655 - val_acc: 0.4039
Epoch 3/20
17737/17737 [==============================] - 2s 88us/step - loss: 2.0605 - acc: 0.4424 - val_loss: 1.9720 - val_acc: 0.4607
Epoch 4/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.8226 - acc: 0.4875 - val_loss: 1.8851 - val_acc: 0.4815
Epoch 5/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.7066 - acc: 0.5134 - val_loss: 1.8263 - val_acc: 0.4881
Epoch 6/20
17737/17737 [==============================] - 2s 89us/step - loss: 1.6192 - acc: 0.5321 - val_loss: 1.8192 - val_acc: 0.4774
Epoch 7/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.5575 - acc: 0.5450 - val_loss: 1.7760 - val_acc: 0.4866
Epoch 8/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.4942 - acc: 0.5611 - val_loss: 1.8054 - val_acc: 0.4845
Train on 17737 samples, validate on 1971 samples
Epoch 1/20
17737/17737 [==============================] - 4s 247us/step - loss: 3.8863 - acc: 0.0399 - val_loss: 3.7864 - val_acc: 0.0523
Epoch 2/20
17737/17737 [==============================] - 2s 89us/step - loss: 3.6404 - acc: 0.0807 - val_loss: 3.2741 - val_acc: 0.1593
Epoch 3/20
17737/17737 [==============================] - 2s 88us/step - loss: 2.6694 - acc: 0.2982 - val_loss: 2.2147 - val_acc: 0.4196
Epoch 4/20
17737/17737 [==============================] - 2s 90us/step - loss: 2.0886 - acc: 0.4351 - val_loss: 1.9374 - val_acc: 0.4587
Epoch 5/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.9286 - acc: 0.4657 - val_loss: 1.8809 - val_acc: 0.4642
Epoch 6/20
17737/17737 [==============================] - 2s 89us/step - loss: 1.8267 - acc: 0.4868 - val_loss: 1.8035 - val_acc: 0.4795
Epoch 7/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.7672 - acc: 0.5032 - val_loss: 1.7949 - val_acc: 0.4926
Epoch 8/20
17737/17737 [==============================] - 2s 89us/step - loss: 1.7040 - acc: 0.5120 - val_loss: 1.8211 - val_acc: 0.4820
Epoch 9/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.6542 - acc: 0.5267 - val_loss: 1.7644 - val_acc: 0.4835
Epoch 10/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.6185 - acc: 0.5311 - val_loss: 1.7925 - val_acc: 0.4774
Train on 17737 samples, validate on 1971 samples
Epoch 1/20
17737/17737 [==============================] - 4s 253us/step - loss: 3.8601 - acc: 0.0457 - val_loss: 3.7202 - val_acc: 0.0583
Epoch 2/20
17737/17737 [==============================] - 2s 89us/step - loss: 3.5077 - acc: 0.1113 - val_loss: 2.7290 - val_acc: 0.2719
Epoch 3/20
17737/17737 [==============================] - 2s 89us/step - loss: 2.3208 - acc: 0.3848 - val_loss: 2.0343 - val_acc: 0.4500
Epoch 4/20
17737/17737 [==============================] - 2s 89us/step - loss: 1.9541 - acc: 0.4653 - val_loss: 1.8710 - val_acc: 0.4855
Epoch 5/20
17737/17737 [==============================] - 2s 90us/step - loss: 1.8113 - acc: 0.4916 - val_loss: 1.8289 - val_acc: 0.4891
Epoch 6/20
17737/17737 [==============================] - 2s 90us/step - loss: 1.7284 - acc: 0.5079 - val_loss: 1.7833 - val_acc: 0.4911
Epoch 7/20
17737/17737 [==============================] - 2s 89us/step - loss: 1.6668 - acc: 0.5283 - val_loss: 1.7587 - val_acc: 0.4850
Epoch 8/20
17737/17737 [==============================] - 2s 91us/step - loss: 1.6190 - acc: 0.5327 - val_loss: 1.7580 - val_acc: 0.4937
Epoch 9/20
17737/17737 [==============================] - 2s 93us/step - loss: 1.5612 - acc: 0.5463 - val_loss: 1.7718 - val_acc: 0.4769
Epoch 10/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.5229 - acc: 0.5516 - val_loss: 1.7691 - val_acc: 0.4921
Epoch 11/20
17737/17737 [==============================] - 2s 88us/step - loss: 1.4876 - acc: 0.5637 - val_loss: 1.7732 - val_acc: 0.4830
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 8s 116us/step - loss: 3.0864 - acc: 0.1940 - val_loss: 2.2558 - val_acc: 0.3590
Epoch 2/20
70948/70948 [==============================] - 6s 78us/step - loss: 1.8851 - acc: 0.4430 - val_loss: 1.9061 - val_acc: 0.4277
Epoch 3/20
70948/70948 [==============================] - 5s 77us/step - loss: 1.7476 - acc: 0.4745 - val_loss: 1.8784 - val_acc: 0.4424
Epoch 4/20
70948/70948 [==============================] - 5s 77us/step - loss: 1.6750 - acc: 0.4940 - val_loss: 1.8199 - val_acc: 0.4495
Epoch 5/20
70948/70948 [==============================] - 6s 79us/step - loss: 1.6211 - acc: 0.5108 - val_loss: 1.8232 - val_acc: 0.4466
Epoch 6/20
70948/70948 [==============================] - 6s 78us/step - loss: 1.5676 - acc: 0.5266 - val_loss: 1.8178 - val_acc: 0.4465
Epoch 7/20
70948/70948 [==============================] - 5s 77us/step - loss: 1.5156 - acc: 0.5433 - val_loss: 1.8995 - val_acc: 0.4409
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 10s 135us/step - loss: 3.1236 - acc: 0.1884 - val_loss: 2.1751 - val_acc: 0.3743
Epoch 2/20
70948/70948 [==============================] - 6s 89us/step - loss: 1.9477 - acc: 0.4262 - val_loss: 1.8723 - val_acc: 0.4343
Epoch 3/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.7996 - acc: 0.4621 - val_loss: 1.8103 - val_acc: 0.4505
Epoch 4/20
70948/70948 [==============================] - 6s 89us/step - loss: 1.7300 - acc: 0.4794 - val_loss: 1.8094 - val_acc: 0.4490
Epoch 5/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.6806 - acc: 0.4927 - val_loss: 1.8066 - val_acc: 0.4633
Epoch 6/20
70948/70948 [==============================] - 6s 89us/step - loss: 1.6418 - acc: 0.5029 - val_loss: 1.7866 - val_acc: 0.4573
Epoch 7/20
70948/70948 [==============================] - 6s 89us/step - loss: 1.6066 - acc: 0.5132 - val_loss: 1.7840 - val_acc: 0.4611
Epoch 8/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.5761 - acc: 0.5222 - val_loss: 1.7756 - val_acc: 0.4644
Epoch 9/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.5438 - acc: 0.5320 - val_loss: 1.8019 - val_acc: 0.4652
Epoch 10/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.5172 - acc: 0.5394 - val_loss: 1.7733 - val_acc: 0.4675
Epoch 11/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.4850 - acc: 0.5501 - val_loss: 1.8655 - val_acc: 0.4614
Epoch 12/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.4592 - acc: 0.5577 - val_loss: 1.8074 - val_acc: 0.4554
Epoch 13/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.4310 - acc: 0.5666 - val_loss: 1.8676 - val_acc: 0.4595
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 10s 142us/step - loss: 3.4661 - acc: 0.1156 - val_loss: 2.4634 - val_acc: 0.3106
Epoch 2/20
70948/70948 [==============================] - 6s 91us/step - loss: 2.1537 - acc: 0.3830 - val_loss: 1.9668 - val_acc: 0.4169
Epoch 3/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.9434 - acc: 0.4273 - val_loss: 1.8850 - val_acc: 0.4277
Epoch 4/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.8623 - acc: 0.4462 - val_loss: 1.8741 - val_acc: 0.4377
Epoch 5/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.8091 - acc: 0.4600 - val_loss: 1.8333 - val_acc: 0.4384
Epoch 6/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.7757 - acc: 0.4664 - val_loss: 1.7718 - val_acc: 0.4556
Epoch 7/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.7477 - acc: 0.4744 - val_loss: 1.7594 - val_acc: 0.4650
Epoch 8/20
70948/70948 [==============================] - 6s 90us/step - loss: 1.7259 - acc: 0.4806 - val_loss: 1.7597 - val_acc: 0.4627
Epoch 9/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.7068 - acc: 0.4856 - val_loss: 1.7402 - val_acc: 0.4658
Epoch 10/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.6921 - acc: 0.4880 - val_loss: 1.7439 - val_acc: 0.4651
Epoch 11/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.6789 - acc: 0.4941 - val_loss: 1.7528 - val_acc: 0.4623
Epoch 12/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.6646 - acc: 0.4976 - val_loss: 1.7476 - val_acc: 0.4587
Train on 70948 samples, validate on 7884 samples
Epoch 1/20
70948/70948 [==============================] - 10s 138us/step - loss: 3.3954 - acc: 0.1317 - val_loss: 2.2398 - val_acc: 0.3598
Epoch 2/20
70948/70948 [==============================] - 6s 91us/step - loss: 2.0720 - acc: 0.4007 - val_loss: 1.9219 - val_acc: 0.4210
Epoch 3/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.8821 - acc: 0.4419 - val_loss: 1.8437 - val_acc: 0.4424
Epoch 4/20
70948/70948 [==============================] - 7s 92us/step - loss: 1.8031 - acc: 0.4612 - val_loss: 1.8018 - val_acc: 0.4512
Epoch 5/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.7591 - acc: 0.4695 - val_loss: 1.7711 - val_acc: 0.4600
Epoch 6/20
70948/70948 [==============================] - 7s 92us/step - loss: 1.7179 - acc: 0.4827 - val_loss: 1.7575 - val_acc: 0.4612
Epoch 7/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.6899 - acc: 0.4906 - val_loss: 1.7955 - val_acc: 0.4557
Epoch 8/20
70948/70948 [==============================] - 6s 91us/step - loss: 1.6667 - acc: 0.4970 - val_loss: 1.7643 - val_acc: 0.4592
Epoch 9/20
70948/70948 [==============================] - 7s 92us/step - loss: 1.6423 - acc: 0.5025 - val_loss: 1.7553 - val_acc: 0.4602
527.96875
Commentaire sur l’apprentissage :
Pour les modèles sans DA :
- Les modèles sans dropout sont plus rapides à entrainer : 8 Epoch pour base, 10 Epoch pour dropout_01, 12 Epoch pour dropout_03.
- Étrangement le dropout_L (avec un dropout cumulé inférieur à dropout_03) met 13 Epoch (donc plus que dropout_03)
Pour les modèles avec DA (4 fois plus d’exemples) :
- le modèle de base met plus d’ Epoch (11) que sans DA, bien que le nombre d’exemples soit 4 fois plus important
- le modèle dropout_01 met seulement 8 Epoch à s’entrainer, c’est moins que sans DA. Peut être que ce taux de drop produit des effets intéressants sur le réseau (pour le type de problématique que nous avons ici)
- Le dropout_03 met plus d’Epoch à l’entrainer
- Le dropout_L met le même nombre d’Epoch (c’est le seul qui n’a pas bougé)
Visualisation de l’accuracy sur le test :
labels = []
plt.figure(figsize=(15,8))
for i in np.arange(0,len(Historique_all)):
plt.plot(np.arange(0,len(Historique_all[i].history["val_acc"])), Historique_all[i].history["val_acc"])
plt.legend(np.array(Name_list))
<matplotlib.legend.Legend at 0x1c2b4683630>

for i in np.arange(0,len(Historique_all)):
if i == 0:
df_data = pd.DataFrame(data = Historique_all[i].history)
df_data["Model"] = Name_list[i]
else:
df_datatmp = pd.DataFrame(data = Historique_all[i].history)
df_datatmp["Model"] = Name_list[i]
df_data = pd.concat([df_data,df_datatmp])
sns.set(style="whitegrid")
plt.figure(figsize=(15,8))
sns.barplot(x="Model", y="val_acc", data=df_data , estimator= max)
<matplotlib.axes._subplots.AxesSubplot at 0x1c4d0d03c50>

Commentaire sur les graphiques de “Val_acc” (acuracy sur le test):
Systématiquement l’accuracy des réseaux entrainés sans DA est meilleur.
ARI : merci de trouver une explication plausible hahah…
Nous pensons que cela vient de la structure des données : les exemples du CSV blabla
Simulations des parties entres NN
Etape 0 : test de tous les NN contre des bots MC
Pour avoir plus d’info sur la performance et le comportement des réseaux on commence par le faire jouer chacun contre un bot Monte-Carlo.
n_game = 100
niter = 100
Loser_badmove_MC = []
HistoWinner_MC = []
Histo_quel_NN_MC = []
for m in np.arange(0,len(Model_list)):
for i in np.arange(0,n_game):
damier = np.zeros((8, 8))
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
x,y = MC_VS_NN2_histo(damier, player, Model_list[m], niter, Name_list[m])
else :
x,y = MC_VS_NN1_histo(damier, player, Model_list[m], niter, Name_list[m])
Loser_badmove_MC.append(x)
HistoWinner_MC.append(y)
Histo_quel_NN_MC.append(Name_list[m])
print(Name_list[m])
base
base_drop_01
base_drop_03
base_drop_L
baseDA
base_drop_01DA
base_drop_03DA
base_drop_LDA
H01 = pd.DataFrame(np.array(Loser_badmove_MC)[:,0] , columns = ["Nombre de défaites"])
print(H01.shape)
sns.set(style = "darkgrid")
sns.countplot(x = "Nombre de défaites",data = H01)
(800, 1)
<matplotlib.axes._subplots.AxesSubplot at 0x1c4d38c2b00>

le MC perds quasiment toutes se le MC gagne quelques parties contre le NN avec un dropout de 0.3 et la Data augmentation… c est assez bizzare, on verifira en réentrainant
d = {"BadMove" : np.array(Loser_badmove_MC)[:,1].astype("int32"), "NomNN":np.array(Histo_quel_NN_MC) }
checkbad = pd.DataFrame(d)
#plt.figure(figsize=(20,10))
#ax = sns.barplot(x="NomNN", y="BadMove", data=checkbad)
print(np.sum(checkbad.iloc[:,0]))
checkbad.shape
0
(800, 2)
Les NN ne tentent pas de coups interdits quand ils jouent contre des bot MC (contrairement à precedement contre le bot random)
Etape 1 : Faire jouer chaque réseau contre lui même
Afin de contrôler les algorithmes et le comportement des NN on fait maintenant se battre le même réseau contre lui-même :
- Pour rappel nous avons un double aléa sur l’initialisation des parties (sur qui commence et sur sa position de jeu)
- Chaques réseau devrat avoir 50% de probabilité de gagner contre lui même (comme le jeux est equilibré)
Pour vérifier cela, les réseaux sont labélisés H et V selon qu’ils jouent verticalement ou horizontalement. Les réseaux notés ainsi se battent contre eux-mêmes.
n_game = 100
niter = 100
Loser_badmove_Same_NN = []
HistoWinner_Same_NN = []
Histo_quel_NN_Same_NN = []
for m0 in np.arange(0,len(Model_list)):
m1=m0
for i in np.arange(0,n_game):
damier = np.zeros((8, 8))
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
x,y = NN_VS_NN(damier, player, Model_list[m0] , Model_list[m1],(Name_list[m0]+"V"),(Name_list[m1]+"H"))
else:
x,y = NN_VS_NN(damier, player, Model_list[m1] , Model_list[m0],(Name_list[m1]+"V"),(Name_list[m0]+"H"))
Loser_badmove_Same_NN.append(x)
HistoWinner_Same_NN.append(y)
Histo_quel_NN_Same_NN.append((Name_list[m0],Name_list[m1],x[0]))
Visualisation du nombre de défaites des NN:
def graph_bar_defaites(Histo):
H02 = pd.DataFrame(np.array(Histo)[:,2] , columns = ["Réseau"])
plt.figure(figsize=(12,8))
H02["% de defaites"] = 1
df_defaite_solo_G1 = 100*pd.pivot_table(H02, index = ["Réseau"], values = ["% de defaites"], aggfunc = np.sum )/(n_game)
df_defaite_solo_G1.sort_values(["Réseau"]).plot.bar()
H02 = pd.DataFrame(np.array(Histo_quel_NN_Same_NN)[:,2] , columns = ["Réseau"])
H02.shape
(800, 1)
graph_bar_defaites(Histo_quel_NN_Same_NN)
<Figure size 864x576 with 0 Axes>

Étrangement, l’on constate que certains réseaux lorsqu’ ils jouent contre eux-mêmes ont deux sortes de comportements :
Un nombre de défaites relativement équivalent pour le réseau jouant V et celui jouant H : Le réseau jouant contre lui-même est aussi performant dans les deux sens de jeux (count = +/- 50)
Toutes les défaites uniquement dans le même sens de jeux : Le réseau jouant contre lui-même perd systématiquement dans un sens (count = 100).
De plus si l’on ré entraine les réseaux (avec les mêmes données), ce ne sont pas les mêmes modèles de NN qui jouent de façon déséquilibrée. Ainsi cela semble mettre en évidence que les conditions d’initialisation des réseaux et l’ordre des exemples ont une influence sur le comportement du réseau.
Etape 3 : Faire jouer chaque réseau contre les autres reseaux
n_game = 200
Loser_badmove_NN_VS_NN = []
HistoWinner_NN_VS_NN = []
Histo_quel_NN_NN_VS_NN = []
for m0 in np.arange(0,len(Model_list)):
for m1 in np.arange(0,len(Model_list)):
if m0 != m1:
for i in np.arange(0,n_game):
damier = np.zeros((8, 8)) #tester avec des etats aléatoirs apres
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
a,b = (Name_list[m0]),(Name_list[m1])
x,y = NN_VS_NN(damier, player, Model_list[m0] , Model_list[m1],a,b)
else:
b,a = (Name_list[m1]),(Name_list[m0])
x,y = NN_VS_NN(damier, player, Model_list[m1] , Model_list[m0],b,a)
Loser_badmove_NN_VS_NN.append(x)
HistoWinner_NN_VS_NN.append(y)
Histo_quel_NN_NN_VS_NN.append((a,b,x[0]))
print(m0, "/",len(Model_list)-1)
0 / 7
1 / 7
2 / 7
3 / 7
4 / 7
5 / 7
6 / 7
7 / 7
H03 = pd.DataFrame(np.array(Histo_quel_NN_NN_VS_NN)[:,2] , columns = ["Réseau"])
plt.figure(figsize=(12,8))
H03["% de defaites"] = 1
df_defaite_G1 = 100*pd.pivot_table(H03, index = ["Réseau"], values = ["% de defaites"], aggfunc = np.sum )/(len(Model_list)*2*n_game)
df_defaite_G1.sort_values(["% de defaites"]).plot.bar()
<matplotlib.axes._subplots.AxesSubplot at 0x1c5221bb668>
<Figure size 864x576 with 0 Axes>

En faisant jouer les NN contre les autres NN :
- Les NN avec Data Augmentation (DA) ont le moins de défaites : entre 30 et 40%
- Les NN sans DA font environ 50% de défaites, sauf pour le NN de base avec 60%
Le fait que réseaux fassent presque exactement 50% de défaites est surprenants : cela laisse penser que les conditions de début de partie ont une influence sur les résultats. On creuse cette idée dans regardant les scores entre chaque NN.
def graph_2DWinners(Histo_quel_NN_NN_VS_NN):
df_result = pd.DataFrame(data= Histo_quel_NN_NN_VS_NN , columns = ["player_1","player_2","Looser" ] )
df_result["P1_win"] = (df_result["player_2"] == df_result["Looser"]).astype("int16")
df_result["P2_win"] = (df_result["player_1"] == df_result["Looser"]).astype("int16")
df_result_game = pd.pivot_table(df_result, "P1_win" , "player_1" , "player_2")
plt.figure(figsize=(12,8), dpi= 80)
sns.heatmap(df_result_game, xticklabels=Name_list, yticklabels=Name_list, cmap='RdYlGn', center=0, annot=True)
plt.title('Taux de victoires par affrontement entre NN', fontsize=18)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
graph_2DWinners(Histo_quel_NN_NN_VS_NN)

Les match entre les NN sont représentés sous la forme d’une matrice 2D, les lignes correspondent aux taux de victoires des NN contres les NN en colonnes
Configuration des parties
- Chaque réseau de nombreuses parties contre chaque autres réseaux .
- Les prédictions des NN sont déterministes une fois le réseau entrainé, il jouera toujours pareil selon l’état du board.
- Cela va aussi pour le premier coup de la partie et donc tous les coups suivants et pour toute la partie. l’état initiale du board erst donc déterminant sur la suite de la partie
Ainsi comme nous avons un double aléa sur le début de partie : sur la position de jeux et sur qui joue en premier. On observe donc, à un petit aléa pres, que les NN gagnent à 0%, 25%, 50%, 75% ou 100% contre les autres réseaux. Cela veut dire que le réseau joue de façon systématiquement supérieure pour une configuration de départ.
Afin de confirmer que les parties jouées par les réseaux se déroulent de la même façon si le début de partie est le même, on regarde peut regarder le nombre de coups uniques dans les historiques enregistrés
#pour remettre les data des parties dans le meme format que le csv
def format_allGame(out_game_level0):
x1 = format_output(out_game_level0[0])
for i in np.arange(0,len(out_game_level0)):
x1 = np.vstack((x1, format_output(out_game_level0[i])))
return x1
def format_output(out_game_level1):
x1 = format_OneGame(out_game_level1[0])
for i in np.arange(len(out_game_level1)):
x1 = np.vstack((x1, format_OneGame(out_game_level1[i])))
return x1
def format_OneGame(game_list_lvl2):
x = np.append(np.array(game_list_lvl2[0]).ravel(),np.array(game_list_lvl2[1]).ravel())
y = np.append(np.array(game_list_lvl2[2]).ravel(),np.array(game_list_lvl2[3]).ravel())
return np.append(x,y).reshape(1,256)
Les historiques des parties sont remis dans un format standardisé (le même que le csv)
GameFormated_NN_VS_NN = format_allGame(HistoWinner_NN_VS_NN)
print(GameFormated_NN_VS_NN.shape)
np.unique(GameFormated_NN_VS_NN, axis = 0).shape # shape(1638, 256)
(182482, 256)
(1716, 256)
print(182945/1467)
124.70688479890934
Moins de 1 coup sur 100 sont uniques dans les parties jou par les NN avec un damier vide en début de partie. Cela confirme que dans ces conditions de départ les NN jouent toujours pareil et les parties se répètent.
GameFormated_MC100 = format_allGame(HistoWinner_MC)
print(GameFormated_MC100.shape) #(10815, 256)
print(np.unique(GameFormated_MC100, axis = 0).shape) #(361, 256)
print(10815/361)
(10937, 256)
(370, 256)
29.958448753462605
À titre de comparaison, on regarde maintenant le nombre de coups uniques lors des parties de réseaux contre les bot MC avec un ratio de 1/30 on est plus bas que dans le cas précédent : les parties sont tout de même assez similaires, les conditions de départ (damier vide) va engendrer des parties presque toutes pareilles également.
Etape 3B : Faire jouer chaque réseau contre les autres reseaux - premiers coups random
On voudrait tester la capacité des NN à jouer plus de configuration différente, pour mieux évaluer leurs performances et surtout pour augmenter les données d’apprentissages. Ainsi on impose que les deux coups de départ soient choisis de façon aléatoire.
#jouer avec 2 coups random au début
n_game3 = 200
n_game = n_game3
Loser_badmove_NN_VS_NN_randStart = []
HistoWinner_NN_VS_NN_randStart = []
Histo_quel_NN_NN_VS_NN_randStart = []
for m0 in np.arange(0,len(Model_list)):
for m1 in np.arange(0,len(Model_list)):
for i in np.arange(0,n_game):
if m0 != m1:
damier = np.zeros((8, 8))
play = random.choice(coups_possibles_H(damier)) #coup random
coup_H(damier, play[0], play[1])
play = random.choice(coups_possibles_V(damier)) #coup random
coup_V(damier, play[0], play[1])
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
a,b = (Name_list[m0]),(Name_list[m1])
x,y = NN_VS_NN(damier, player, Model_list[m0] , Model_list[m1],a,b)
else:
b,a = (Name_list[m1]),(Name_list[m0])
x,y = NN_VS_NN(damier, player, Model_list[m1] , Model_list[m0],b,a)
Loser_badmove_NN_VS_NN_randStart.append(x)
HistoWinner_NN_VS_NN_randStart.append(y)
Histo_quel_NN_NN_VS_NN_randStart.append((a,b,x[0]))
print(m0, "/",len(Model_list)-1)
0 / 7
1 / 7
2 / 7
3 / 7
4 / 7
5 / 7
6 / 7
7 / 7
H03 = pd.DataFrame(np.array(Histo_quel_NN_NN_VS_NN_randStart)[:,2] , columns = ["Réseau"])
plt.figure(figsize=(12,8))
H03["% de defaites"] = 1
df_defaite_G1 = 100*pd.pivot_table(H03, index = ["Réseau"], values = ["% de defaites"], aggfunc = np.sum )/(len(Model_list)*2*n_game)
df_defaite_G1.sort_values(["% de defaites"]).plot.bar()
<matplotlib.axes._subplots.AxesSubplot at 0x1c521f43d68>
<Figure size 864x576 with 0 Axes>

df_result = pd.DataFrame(data= Histo_quel_NN_NN_VS_NN_randStart , columns = ["player_1","player_2","Looser" ] )
df_result["P1_win"] = (df_result["player_2"] == df_result["Looser"]).astype("int16")
df_result["P2_win"] = (df_result["player_1"] == df_result["Looser"]).astype("int16")
df_result_game = pd.pivot_table(df_result, "P1_win" , "player_1" , "player_2")
plt.figure(figsize=(12,8), dpi= 80)
sns.heatmap(df_result_game, xticklabels=Name_list, yticklabels=Name_list, cmap='RdYlGn', center=0, annot=True,vmin=0, vmax=1)
plt.title('Taux de victoires par affrontement entre NN - random start', fontsize=18)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
(array([0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5, 7.5]),
<a list of 8 Text yticklabel objects>)

Interprétation des taux de victoire des NN avec début de parties aléatoires :
- On constate dans le bar plat que les NN ne se distinguent pas particulièrement dans leur capacité à mieux jouer que les autres : les taux de défaites des NN sont compris entre 40% et 60%
- Idem pour le plot 2D des taux de victoires, aucun NN ne sort du lot et tous gagnent entre 35% et 65% de leurs matchs
Nous essayons maintenant de réentrainer les NN avec plus d’exemples issus des coups uniques joués lors de ces parties.
GameFormated_NN_VS_NN_randStart = format_allGame(HistoWinner_NN_VS_NN_randStart)
print(GameFormated_NN_VS_NN_randStart.shape) #(166414, 256)
np.unique(GameFormated_NN_VS_NN_randStart, axis = 0).shape #(145234, 256)
(165932, 256)
(144924, 256)
On constate que cette fois-ci, les historiques de parties joués avec les 2 premiers coups aléatoires sont des coups uniques à plus de 80%.
Préparation des données pour re entraines les NN
On réentraine les NN avec les données suivantes:
- Les coups uniques des parties NN VS MC
- Les coups uniques des parties NN VS NN avec random start
- Les coups uniques des parties NN VS NN avec random start
On vérifiera aussi que coups que l’on rajoute ainsi au train ne sont pas déjà présent dans le test (pour ne pas fausser les scores)
train_gen2 = pd.DataFrame(train)
train_all = pd.concat([train_gen2,pd.DataFrame(GameFormated_MC100),pd.DataFrame(GameFormated_NN_VS_NN),pd.DataFrame(GameFormated_NN_VS_NN_randStart)])
print(train_all.shape)
train_all = train_all.drop_duplicates()
print(train_all.shape)
(379059, 256)
(165477, 256)
Le nouveau train issus des parties jouée et du CSV contient beaucoup plus de coups. On retire les coups qui seraient présent dans le train
train_all_np = np.array(train_all)
test_np = np.array(test)
aset = set([tuple(x) for x in train_all_np])
bset = set([tuple(x) for x in test_np])
intersect = [x for x in aset & bset]
print(np.array(intersect).shape)
(190, 256)
Effectivement on retrouve une centaine de coup du test dans le nouveaux coups générés pour le train, ils sont retirés
Train_G2 = []
for x in aset:
if not (x in intersect):
Train_G2.append(x)
random.shuffle(Train_G2)
Entrainement des NN sur les données enrichis des parties précédentes (Génération 2)
X_train_DA_NO_G2,Y_train_DA_NO_G2,X_test_DA_NO_G2,Y_test_DA_NO_G2 = prepare_train_DA_NO(Train_G2,test)
X_train_DA_YES_G2,Y_train_DA_YES_G2,X_test_DA_YES_G2,Y_test_DA_YES_G2 = prepare_train_DA_YES(Train_G2,test)
X_train_DA_NO_G2
array([[[[0., 1., 1.],
[1., 0., 1.],
[0., 1., 1.],
...,
[0., 1., 1.],
[0., 1., 1.],
[0., 1., 1.]],
[[0., 1., 1.],
[1., 0., 1.],
[0., 1., 1.],
...,
[0., 1., 1.],
[0., 1., 1.],
[0., 1., 1.]],
[[0., 1., 1.],
[0., 1., 1.],
[0., 1., 1.],
...,
[0., 1., 1.],
[0., 1., 1.],
[0., 1., 1.]],
...,
X_train_DA_YES_G2.shape
(661148, 8, 8, 3)
['base_G2',
'base_drop_01_G2',
'base_drop_03_G2',
'base_drop_L_G2',
'baseDA_G2',
'base_drop_01DA_G2',
'base_drop_03DA_G2',
'base_drop_LDA_G2']
Model_list_G2 = []
Name_list = ["base","base_drop_01","base_drop_03","base_drop_L","baseDA","base_drop_01DA","base_drop_03DA","base_drop_LDA" ]
Name_list_G2 = [N + '_G2' for N in Name_list]
Model_list_G2.append(get_model_base())
Model_list_G2.append(get_model_dropout_01())
Model_list_G2.append(get_model_dropout_03())
Model_list_G2.append(get_model_dropout_L())
Model_list_G2.append(get_model_base())
Model_list_G2.append(get_model_dropout_01())
Model_list_G2.append(get_model_dropout_03())
Model_list_G2.append(get_model_dropout_L())
Historique_all_G2 = []
Historique_all_G2.append(Keras_training(Model_list_G2[0],X_train_DA_NO_G2,Y_train_DA_NO_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[1],X_train_DA_NO_G2,Y_train_DA_NO_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[2],X_train_DA_NO_G2,Y_train_DA_NO_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[3],X_train_DA_NO_G2,Y_train_DA_NO_G2))
#Historique_all_G2.append(Keras_training(Model_list_G2[4],X_train_DA_YES_G2,Y_train_DA_YES_G2))
#Historique_all_G2.append(Keras_training(Model_list_G2[5],X_train_DA_YES_G2,Y_train_DA_YES_G2))
#Historique_all_G2.append(Keras_training(Model_list_G2[6],X_train_DA_YES_G2,Y_train_DA_YES_G2))
#Historique_all_G2.append(Keras_training(Model_list_G2[7],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Train on 148758 samples, validate on 16529 samples
Epoch 1/20
148758/148758 [==============================] - 17s 112us/step - loss: 1.8475 - acc: 0.4906 - val_loss: 1.5296 - val_acc: 0.5554
Epoch 2/20
148758/148758 [==============================] - 12s 82us/step - loss: 1.2509 - acc: 0.6193 - val_loss: 1.2935 - val_acc: 0.6074
Epoch 3/20
148758/148758 [==============================] - 12s 82us/step - loss: 1.1695 - acc: 0.6369 - val_loss: 1.2523 - val_acc: 0.6202
Epoch 4/20
148758/148758 [==============================] - 12s 82us/step - loss: 1.1154 - acc: 0.6493 - val_loss: 1.2956 - val_acc: 0.6030
Epoch 5/20
148758/148758 [==============================] - 12s 81us/step - loss: 1.0693 - acc: 0.6611 - val_loss: 1.2167 - val_acc: 0.6199
Epoch 6/20
148758/148758 [==============================] - 12s 82us/step - loss: 1.0268 - acc: 0.6723 - val_loss: 1.2246 - val_acc: 0.6226
Epoch 7/20
148758/148758 [==============================] - 12s 82us/step - loss: 0.9871 - acc: 0.6827 - val_loss: 1.2170 - val_acc: 0.6241
Epoch 8/20
148758/148758 [==============================] - 12s 82us/step - loss: 0.9463 - acc: 0.6937 - val_loss: 1.2235 - val_acc: 0.6261
Epoch 9/20
148758/148758 [==============================] - 12s 81us/step - loss: 0.9066 - acc: 0.7054 - val_loss: 1.3028 - val_acc: 0.6191
Epoch 10/20
148758/148758 [==============================] - 12s 82us/step - loss: 0.8673 - acc: 0.7166 - val_loss: 1.2607 - val_acc: 0.6165
Epoch 11/20
148758/148758 [==============================] - 12s 82us/step - loss: 0.8260 - acc: 0.7287 - val_loss: 1.2783 - val_acc: 0.6173
Train on 148758 samples, validate on 16529 samples
Epoch 1/20
148758/148758 [==============================] - 18s 119us/step - loss: 1.9135 - acc: 0.4756 - val_loss: 1.3643 - val_acc: 0.5929
Epoch 2/20
148758/148758 [==============================] - 14s 93us/step - loss: 1.3097 - acc: 0.6032 - val_loss: 1.3035 - val_acc: 0.6063
Epoch 3/20
148758/148758 [==============================] - 14s 94us/step - loss: 1.2307 - acc: 0.6206 - val_loss: 1.2478 - val_acc: 0.6138
Epoch 4/20
148758/148758 [==============================] - 14s 93us/step - loss: 1.1852 - acc: 0.6319 - val_loss: 1.2205 - val_acc: 0.6223
Epoch 5/20
148758/148758 [==============================] - 14s 95us/step - loss: 1.1499 - acc: 0.6396 - val_loss: 1.2394 - val_acc: 0.6172
Epoch 6/20
148758/148758 [==============================] - 14s 96us/step - loss: 1.1213 - acc: 0.6466 - val_loss: 1.1880 - val_acc: 0.6289
Epoch 7/20
148758/148758 [==============================] - 14s 95us/step - loss: 1.0964 - acc: 0.6521 - val_loss: 1.1858 - val_acc: 0.6291
Epoch 8/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.0770 - acc: 0.6581 - val_loss: 1.1713 - val_acc: 0.6339
Epoch 9/20
148758/148758 [==============================] - 15s 98us/step - loss: 1.0560 - acc: 0.6634 - val_loss: 1.1827 - val_acc: 0.6312
Epoch 10/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.0394 - acc: 0.6681 - val_loss: 1.1859 - val_acc: 0.6376
Epoch 11/20
148758/148758 [==============================] - 14s 95us/step - loss: 1.0252 - acc: 0.6710 - val_loss: 1.1887 - val_acc: 0.6305
Epoch 12/20
148758/148758 [==============================] - 14s 95us/step - loss: 1.0105 - acc: 0.6741 - val_loss: 1.1696 - val_acc: 0.6296
Epoch 13/20
148758/148758 [==============================] - 14s 95us/step - loss: 0.9955 - acc: 0.6781 - val_loss: 1.1845 - val_acc: 0.6300
Train on 148758 samples, validate on 16529 samples
Epoch 1/20
148758/148758 [==============================] - 18s 122us/step - loss: 2.1731 - acc: 0.4187 - val_loss: 1.4263 - val_acc: 0.5863
Epoch 2/20
148758/148758 [==============================] - 14s 96us/step - loss: 1.4241 - acc: 0.5783 - val_loss: 1.3370 - val_acc: 0.6020
Epoch 3/20
148758/148758 [==============================] - 14s 96us/step - loss: 1.3423 - acc: 0.5968 - val_loss: 1.2674 - val_acc: 0.6112
Epoch 4/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.3029 - acc: 0.6051 - val_loss: 1.2255 - val_acc: 0.6210
Epoch 5/20
148758/148758 [==============================] - 14s 96us/step - loss: 1.2767 - acc: 0.6100 - val_loss: 1.2242 - val_acc: 0.6204
Epoch 6/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2559 - acc: 0.6161 - val_loss: 1.2271 - val_acc: 0.6177
Epoch 7/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2429 - acc: 0.6179 - val_loss: 1.2108 - val_acc: 0.6290
Epoch 8/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2310 - acc: 0.6203 - val_loss: 1.1955 - val_acc: 0.6284
Epoch 9/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2208 - acc: 0.6241 - val_loss: 1.2011 - val_acc: 0.6270
Epoch 10/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2144 - acc: 0.6261 - val_loss: 1.1945 - val_acc: 0.6334
Epoch 11/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2073 - acc: 0.6264 - val_loss: 1.2164 - val_acc: 0.6262
Epoch 12/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1998 - acc: 0.6291 - val_loss: 1.1669 - val_acc: 0.6357
Epoch 13/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1969 - acc: 0.6302 - val_loss: 1.1701 - val_acc: 0.6362
Epoch 14/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1909 - acc: 0.6320 - val_loss: 1.1726 - val_acc: 0.6346
Epoch 15/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1868 - acc: 0.6320 - val_loss: 1.1702 - val_acc: 0.6362
Epoch 16/20
148758/148758 [==============================] - 15s 98us/step - loss: 1.1834 - acc: 0.6327 - val_loss: 1.1606 - val_acc: 0.6396
Epoch 17/20
148758/148758 [==============================] - 15s 98us/step - loss: 1.1780 - acc: 0.6350 - val_loss: 1.1724 - val_acc: 0.6336
Epoch 18/20
148758/148758 [==============================] - 15s 98us/step - loss: 1.1758 - acc: 0.6350 - val_loss: 1.1659 - val_acc: 0.6347
Epoch 19/20
148758/148758 [==============================] - 15s 98us/step - loss: 1.1746 - acc: 0.6344 - val_loss: 1.1665 - val_acc: 0.6381
Train on 148758 samples, validate on 16529 samples
Epoch 1/20
148758/148758 [==============================] - 18s 124us/step - loss: 2.0389 - acc: 0.4494 - val_loss: 1.4013 - val_acc: 0.5839
Epoch 2/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.3649 - acc: 0.5924 - val_loss: 1.2821 - val_acc: 0.6134
Epoch 3/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2895 - acc: 0.6073 - val_loss: 1.2402 - val_acc: 0.6091
Epoch 4/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.2466 - acc: 0.6180 - val_loss: 1.2346 - val_acc: 0.6179
Epoch 5/20
148758/148758 [==============================] - 15s 99us/step - loss: 1.2180 - acc: 0.6241 - val_loss: 1.1965 - val_acc: 0.6260
Epoch 6/20
148758/148758 [==============================] - 14s 96us/step - loss: 1.1965 - acc: 0.6298 - val_loss: 1.2044 - val_acc: 0.6194
Epoch 7/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1803 - acc: 0.6329 - val_loss: 1.2128 - val_acc: 0.6245
Epoch 8/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1656 - acc: 0.6366 - val_loss: 1.1780 - val_acc: 0.6337
Epoch 9/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1534 - acc: 0.6401 - val_loss: 1.1910 - val_acc: 0.6296
Epoch 10/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1460 - acc: 0.6413 - val_loss: 1.1621 - val_acc: 0.6381
Epoch 11/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1339 - acc: 0.6443 - val_loss: 1.1644 - val_acc: 0.6363
Epoch 12/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1259 - acc: 0.6470 - val_loss: 1.1701 - val_acc: 0.6353
Epoch 13/20
148758/148758 [==============================] - 14s 97us/step - loss: 1.1192 - acc: 0.6476 - val_loss: 1.1586 - val_acc: 0.6360
Historique_all_G2x = Historique_all_G2[0:4]
#Historique_all_G2.append(Keras_training(Model_list_G2[4],X_train_DA_YES_G2,Y_train_DA_YES_G2))
#Historique_all_G2.append(Keras_training(Model_list_G2[5],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[6],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[7],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Train on 595033 samples, validate on 66115 samples
Epoch 1/20
595033/595033 [==============================] - 60s 101us/step - loss: 2.4854 - acc: 0.2978 - val_loss: 2.0431 - val_acc: 0.3770
Epoch 2/20
595033/595033 [==============================] - 56s 94us/step - loss: 2.0985 - acc: 0.3657 - val_loss: 1.9648 - val_acc: 0.3909
Epoch 3/20
595033/595033 [==============================] - 56s 95us/step - loss: 2.0565 - acc: 0.3743 - val_loss: 1.9394 - val_acc: 0.3962
Epoch 4/20
595033/595033 [==============================] - 57s 96us/step - loss: 2.0376 - acc: 0.3794 - val_loss: 1.9347 - val_acc: 0.3978
Epoch 5/20
595033/595033 [==============================] - 57s 96us/step - loss: 2.0292 - acc: 0.3816 - val_loss: 1.9160 - val_acc: 0.3995
Epoch 6/20
595033/595033 [==============================] - 57s 96us/step - loss: 2.0225 - acc: 0.3831 - val_loss: 1.9061 - val_acc: 0.3992
Epoch 7/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0178 - acc: 0.3843 - val_loss: 1.9100 - val_acc: 0.4017
Epoch 8/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0158 - acc: 0.3855 - val_loss: 1.9066 - val_acc: 0.4032
Epoch 9/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0138 - acc: 0.3864 - val_loss: 1.8961 - val_acc: 0.4044
Epoch 10/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0128 - acc: 0.3864 - val_loss: 1.8989 - val_acc: 0.4061
Epoch 11/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0110 - acc: 0.3870 - val_loss: 1.9042 - val_acc: 0.4024
Epoch 12/20
595033/595033 [==============================] - 59s 99us/step - loss: 2.0110 - acc: 0.3883 - val_loss: 1.8912 - val_acc: 0.4069
Epoch 13/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0122 - acc: 0.3881 - val_loss: 1.8937 - val_acc: 0.4062
Epoch 14/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0111 - acc: 0.3880 - val_loss: 1.8973 - val_acc: 0.4066
Epoch 15/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0110 - acc: 0.3880 - val_loss: 1.8935 - val_acc: 0.4085
Epoch 16/20
595033/595033 [==============================] - 58s 97us/step - loss: 2.0102 - acc: 0.3893 - val_loss: 1.8856 - val_acc: 0.4077
Epoch 17/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0111 - acc: 0.3889 - val_loss: 1.8918 - val_acc: 0.4065
Epoch 18/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0097 - acc: 0.3891 - val_loss: 1.8953 - val_acc: 0.4077
Train on 595033 samples, validate on 66115 samples
Epoch 1/20
595033/595033 [==============================] - 63s 106us/step - loss: 2.3810 - acc: 0.3169 - val_loss: 1.9896 - val_acc: 0.3823
Epoch 2/20
595033/595033 [==============================] - 58s 98us/step - loss: 2.0271 - acc: 0.3799 - val_loss: 1.9264 - val_acc: 0.3956
Epoch 3/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9856 - acc: 0.3891 - val_loss: 1.9057 - val_acc: 0.4019
Epoch 4/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9677 - acc: 0.3936 - val_loss: 1.8873 - val_acc: 0.4080
Epoch 5/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9562 - acc: 0.3969 - val_loss: 1.8776 - val_acc: 0.4112
Epoch 6/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9497 - acc: 0.3984 - val_loss: 1.8783 - val_acc: 0.4099
Epoch 7/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9446 - acc: 0.3998 - val_loss: 1.8647 - val_acc: 0.4131
Epoch 8/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9415 - acc: 0.4012 - val_loss: 1.8833 - val_acc: 0.4105
Epoch 9/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9400 - acc: 0.4018 - val_loss: 1.8611 - val_acc: 0.4138
Epoch 10/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.9374 - acc: 0.4027 - val_loss: 1.8677 - val_acc: 0.4111
Epoch 11/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9354 - acc: 0.4031 - val_loss: 1.8612 - val_acc: 0.4132
Epoch 12/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9362 - acc: 0.4028 - val_loss: 1.8628 - val_acc: 0.4151
Epoch 13/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9366 - acc: 0.4037 - val_loss: 1.8580 - val_acc: 0.4179
Epoch 14/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9332 - acc: 0.4048 - val_loss: 1.8604 - val_acc: 0.4131
Epoch 15/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9354 - acc: 0.4037 - val_loss: 1.8568 - val_acc: 0.4181
Epoch 16/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9344 - acc: 0.4046 - val_loss: 1.8540 - val_acc: 0.4143
Epoch 17/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.9333 - acc: 0.4048 - val_loss: 1.8613 - val_acc: 0.4155
Epoch 18/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.9336 - acc: 0.4052 - val_loss: 1.8547 - val_acc: 0.4146
Historique_all_G2.append(Keras_training(Model_list_G2[4],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Historique_all_G2.append(Keras_training(Model_list_G2[5],X_train_DA_YES_G2,Y_train_DA_YES_G2))
Train on 595033 samples, validate on 66115 samples
Epoch 1/20
595033/595033 [==============================] - 57s 95us/step - loss: 2.2221 - acc: 0.3451 - val_loss: 1.9696 - val_acc: 0.3908
Epoch 2/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.8858 - acc: 0.4086 - val_loss: 1.8795 - val_acc: 0.4075
Epoch 3/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.8239 - acc: 0.4244 - val_loss: 1.8674 - val_acc: 0.4121
Epoch 4/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.7857 - acc: 0.4355 - val_loss: 1.8471 - val_acc: 0.4165
Epoch 5/20
595033/595033 [==============================] - 52s 88us/step - loss: 1.7589 - acc: 0.4427 - val_loss: 1.8377 - val_acc: 0.4215
Epoch 6/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.7367 - acc: 0.4492 - val_loss: 1.8349 - val_acc: 0.4218
Epoch 7/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.7192 - acc: 0.4544 - val_loss: 1.8485 - val_acc: 0.4181
Epoch 8/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.7044 - acc: 0.4589 - val_loss: 1.8511 - val_acc: 0.4226
Epoch 9/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.6917 - acc: 0.4627 - val_loss: 1.8468 - val_acc: 0.4225
Epoch 10/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.6811 - acc: 0.4660 - val_loss: 1.8514 - val_acc: 0.4222
Epoch 11/20
595033/595033 [==============================] - 52s 87us/step - loss: 1.6718 - acc: 0.4684 - val_loss: 1.8550 - val_acc: 0.4193
Train on 595033 samples, validate on 66115 samples
Epoch 1/20
595033/595033 [==============================] - 64s 107us/step - loss: 2.3095 - acc: 0.3292 - val_loss: 1.9592 - val_acc: 0.3909
Epoch 2/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.9589 - acc: 0.3932 - val_loss: 1.8997 - val_acc: 0.4036
Epoch 3/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.9105 - acc: 0.4034 - val_loss: 1.8749 - val_acc: 0.4108
Epoch 4/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.8847 - acc: 0.4108 - val_loss: 1.8664 - val_acc: 0.4104
Epoch 5/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.8695 - acc: 0.4153 - val_loss: 1.8549 - val_acc: 0.4164
Epoch 6/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.8588 - acc: 0.4177 - val_loss: 1.8504 - val_acc: 0.4167
Epoch 7/20
595033/595033 [==============================] - 59s 99us/step - loss: 1.8521 - acc: 0.4201 - val_loss: 1.8395 - val_acc: 0.4175
Epoch 8/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.8463 - acc: 0.4223 - val_loss: 1.8365 - val_acc: 0.4192
Epoch 9/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8420 - acc: 0.4236 - val_loss: 1.8379 - val_acc: 0.4205
Epoch 10/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8391 - acc: 0.4240 - val_loss: 1.8346 - val_acc: 0.4206
Epoch 11/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8381 - acc: 0.4247 - val_loss: 1.8365 - val_acc: 0.4207
Epoch 12/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8352 - acc: 0.4261 - val_loss: 1.8386 - val_acc: 0.4217
Epoch 13/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.8333 - acc: 0.4266 - val_loss: 1.8424 - val_acc: 0.4223
Epoch 14/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.8327 - acc: 0.4269 - val_loss: 1.8367 - val_acc: 0.4233
Epoch 15/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8310 - acc: 0.4273 - val_loss: 1.8394 - val_acc: 0.4227
Epoch 16/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8314 - acc: 0.4279 - val_loss: 1.8344 - val_acc: 0.4224
Epoch 17/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.8311 - acc: 0.4277 - val_loss: 1.8295 - val_acc: 0.4245
Epoch 18/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8292 - acc: 0.4285 - val_loss: 1.8376 - val_acc: 0.4203
Epoch 19/20
595033/595033 [==============================] - 59s 98us/step - loss: 1.8296 - acc: 0.4276 - val_loss: 1.8369 - val_acc: 0.4214
Epoch 20/20
595033/595033 [==============================] - 58s 98us/step - loss: 1.8295 - acc: 0.4286 - val_loss: 1.8342 - val_acc: 0.4217
plt.figure(figsize=(15,8))
for i in np.arange(0,len(Historique_all_G2)):
plt.plot(np.arange(0,len(Historique_all_G2[i].history["val_acc"])), Historique_all_G2[i].history["val_acc"])
plt.legend(np.array(Name_list))
<matplotlib.legend.Legend at 0x1c636371f98>

for i in np.arange(0,7):
if i == 0:
df_data = pd.DataFrame(data = Historique_all_G2[i].history)
df_data["Model"] = Name_list[i]
else:
df_datatmp = pd.DataFrame(data = Historique_all_G2[i].history)
df_datatmp["Model"] = Name_list[i]
df_data = pd.concat([df_data,df_datatmp])
for i in np.arange(0,len(Historique_all_G2)):
if i == 0:
df_data = pd.DataFrame(data = Historique_all_G2[i].history)
df_data["Model"] = Name_list[i]
else:
df_datatmp = pd.DataFrame(data = Historique_all_G2[i].history)
df_datatmp["Model"] = Name_list[i]
df_data = pd.concat([df_data,df_datatmp])
sns.set(style="whitegrid")
plt.figure(figsize=(15,8))
sns.barplot(x="Model", y="val_acc", data=df_data , estimator= max)
<matplotlib.axes._subplots.AxesSubplot at 0x1c4d1082828>

Commentaires:
- L’accuracy sur le jeu de test est plus importante pour les NN entrainées dans DA avec en moyenne 60% contre 40% pour les NN avec DA.
- Par rapport aux NN entrainés précédemment se représente une amélioration pour les NN sans DA et une baisse de performance pour les modèles avec DA. Cela vient probablement du fait que le jeu de test n’a pas été augmenté et donc les prédictions des NN sont meilleures quand ils sont entrainés sur les NN sans DA, notamment maintenant que l’on a beaucoup augmenté la taille des données d’entrainement d’une autre façon (en reprenant les historiques des parties gagnantes).
Il sera néanmoins intéressant de regarder comment les NN performent dans les matches et si la baisse d’accurracy se traduit par un NN jouant moins bien.
Matchs entre les réseaux
Match : NN de la première génération VS 2e génération (G1 VS G2)
#G1 VS G2
n_game = 200
Loser_badmove_NN_VS_NN_G1_VS_G2_randStart = []
HistoWinner_NN_VS_NN_G1_VS_G2_randStart = []
Histo_quel_NN_NN_VS_NN_G1_VS_G2_randStart = []
for m0 in np.arange(0,len(Model_list_G2)):
for m1 in np.arange(0,len(Model_list)):
for i in np.arange(0,n_game):
if True:
damier = np.zeros((8, 8))
play = random.choice(coups_possibles_H(damier)) #coup random
coup_H(damier, play[0], play[1])
play = random.choice(coups_possibles_V(damier)) #coup random
coup_V(damier, play[0], play[1])
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
a,b = (Name_list_G2[m0]),(Name_list[m1])
x,y = NN_VS_NN(damier, player, Model_list[m0] , Model_list_G2[m1],a,b)
else:
b,a = (Name_list_G2[m1]),(Name_list[m0])
x,y = NN_VS_NN(damier, player, Model_list_G2[m1] , Model_list[m0],b,a)
Loser_badmove_NN_VS_NN_G1_VS_G2_randStart.append(x)
HistoWinner_NN_VS_NN_G1_VS_G2_randStart.append(y)
Histo_quel_NN_NN_VS_NN_G1_VS_G2_randStart.append((a,b,x[0]))
print(m0, "/",len(Model_list)-1)
0 / 7
1 / 7
2 / 7
3 / 7
4 / 7
5 / 7
6 / 7
7 / 7
H03 = pd.DataFrame(np.array(Histo_quel_NN_NN_VS_NN_G1_VS_G2_randStart)[:,2] , columns = ["Réseau"])
plt.figure(figsize=(12,8))
H03["% de defaites"] = 1
df_defaite_G1 = 100*pd.pivot_table(H03, index = ["Réseau"], values = ["% de defaites"], aggfunc = np.sum )/(len(Model_list)*n_game)
df_defaite_G1.sort_values(["% de defaites"]).plot.bar()
<matplotlib.axes._subplots.AxesSubplot at 0x1c6be791208>
<Figure size 864x576 with 0 Axes>

Lorsque l’on fait jouer les NN de la 2e génération, nous constatons que les taux de défaites sont tous relativement proches de 50%. Ainsi aucun des réseaux ne se démarque vraiment dans sa capacité à battre les autres et c’est surtout les conditions de départ du damier (initialisation avec 2coups aléatoire) qui déterminent le gagnant.
Faire jouer la 2eme generation contre elle meme
#G1 VS G2
n_game = 200
Loser_badmove_NN_VS_NN_G2_VS_G2_randStart = []
HistoWinner_NN_VS_NN_G2_VS_G2_randStart = []
Histo_quel_NN_NN_VS_NN_G2_VS_G2_randStart = []
for m0 in np.arange(0,len(Model_list_G2)):
for m1 in np.arange(0,len(Model_list_G2)):
for i in np.arange(0,n_game):
if m0 != m1:
damier = np.zeros((8, 8))
play = random.choice(coups_possibles_H(damier)) #coup random
coup_H(damier, play[0], play[1])
play = random.choice(coups_possibles_V(damier)) #coup random
coup_V(damier, play[0], play[1])
player = randint(1,2)
sens = randint(0,1)
if sens == 0:
a,b = (Name_list_G2[m0]),(Name_list_G2[m1])
x,y = NN_VS_NN(damier, player, Model_list_G2[m0] , Model_list_G2[m1],a,b)
else:
b,a = (Name_list_G2[m1]),(Name_list_G2[m0])
x,y = NN_VS_NN(damier, player, Model_list_G2[m1] , Model_list_G2[m0],b,a)
Loser_badmove_NN_VS_NN_G2_VS_G2_randStart.append(x)
HistoWinner_NN_VS_NN_G2_VS_G2_randStart.append(y)
Histo_quel_NN_NN_VS_NN_G2_VS_G2_randStart.append((a,b,x[0]))
print(m0, "/",len(Model_list)-1)
0 / 7
1 / 7
2 / 7
3 / 7
4 / 7
5 / 7
6 / 7
7 / 7
H03 = pd.DataFrame(np.array(Histo_quel_NN_NN_VS_NN_G2_VS_G2_randStart)[:,2] , columns = ["Réseau"])
plt.figure(figsize=(12,8))
H03["% de defaites"] = 1
df_defaite_G1 = 100*pd.pivot_table(H03, index = ["Réseau"], values = ["% de defaites"], aggfunc = np.sum )/((len(Model_list_G2)-1)*2*n_game)
df_defaite_G1.sort_values(["% de defaites"]).plot.bar()
<matplotlib.axes._subplots.AxesSubplot at 0x1c6bf288978>
<Figure size 864x576 with 0 Axes>

Le modèle de base avec Data Augmentation de la génération a le taux de défaites le plus faible. Cependant ce modèle à une Val_Acc d’environ 0.4 qui est bien inférieur à celle des modèles de la G2 sans DA qui sont autour de 0.6. Ainsi l’entrainement du réseau sur le jeu de données augmenté, même s’il fait baisser l’accuracy du modèle, cela produit un NN qui semble mieux réussir à battre les autres.
Conclusion
Nous avons pu apprendre à un réseau à jouer aux dominos grâce à un historique de coups “intelligents” fournis dans les données d’entrainement. Ces données étaient elle-même tirés de simulation de Monte-Carlo dont le fonctionnement pour choisir le meilleur coup est une approche brute force consistant à tester pleins de combinaisons de coups et choisir ceux qui ont le plus de probabilités de mener à une victoire.
Nous avons pu constater que les NN arrivent rapidement à apprendre à jouer ces coups et à battre un bot Monte-Carlo. Cependant en termes de Val_Acc sur les données de test, la première génération ne fait pas mieux que 50%. Ce chiffre reste cependant plutôt bon, car les possibilités de coup à jours sur chaque damier sont relativement conséquentes (surtout en début de partie).
Nous avons ensuite fait jouer les NN contre eux-mêmes afin de voir si les valeurs de Val_acc étaient liées à une capacité à “mieux jouer” et également comment la structure du réseau influence la façon de jouer. Nous n’avons pas constaté de relation notable entre la Val_Acc et les chances de gagner contre les autres réseaux, au contraire, certains NN avec des Val_Acc plus faibles sont plus fortes que ceux avec des Val_Acc 50% plus grandes.
Finalement, nous avons enregistré les coups gagnants des parties pour enrichir le jeu de données fourni à la base et réentraîner les réseaux. Cela à effectives permis de gagner en Val_Acc et de passer de 0.5 à 0.65 pour les meilleurs modèles.
Bien que cette façon d’enrichir les données ait pu augmenter le score de Val_Acc, cela ne semble pas vraiment rentre le NN “plus fort” pour gagner les parties. En effet même si tous les coups que nous avons rajoutés sont issus de coups joués par les NN ayant gagné leur partie, tous ne sont peut-être pas les plus “intelligents” à jouer.
Pour aller plus loin:
- nous aurions pu regarder le nombre de dominos d’avance des gagnants et ne retenir que les parties avec le plus d’avance, et donc surement des coups plus optimisés.
- Également nous aurions pu implémenter du grid search sur les hyperparametres du réseau, notamment les drop_out ou le batch size